2.6. КАРТЫ КАРНО

	Карты карно (схемы Вейча) это наглядное представление логической
функции в виде карты, которая удобна для оптимизации.
С каждой из сторон записывается значения комбинаций переменных так
чтобы в зтом значении менялся один бит при переходе к следующему.

Придумал Морис Карно (Maurice Karnaugh) в 1950 (Bell Labs)

Примеры шаблонов карт Карно (для разного числа переменных):
  

  

  



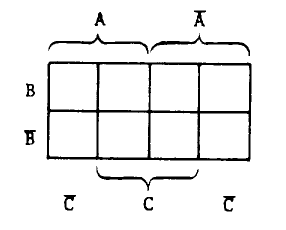
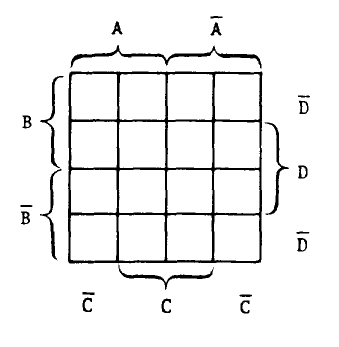
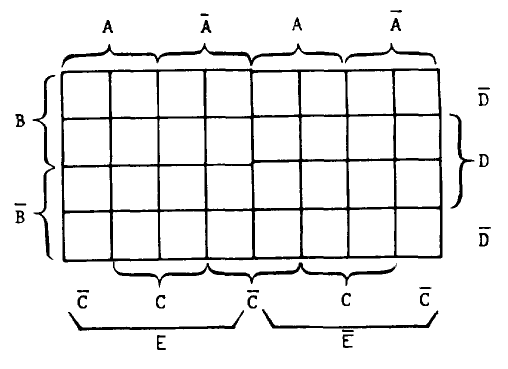
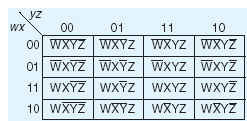
В каждой клетке карты карно находится значение функции, которую описывает 
эта карта на входном наборе соответствующем расположению клетки в карте.



  
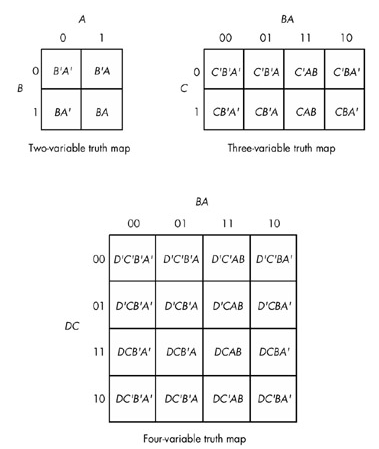
  Пример заполнения (2 переменных) 
 

Собственно сам шаблон карты:

            x2
	 -------
          0   1
	+---+---+
    | 0 |   |   |
  x1|   +---+---+
    | 1 |   |   |
        +---+---+



Предположим мы хотим сделать карту для функции AND.
Берем таблицу истинности:

	x2 x1  | AND
	-------+-----
	0  0   | 0
	0  1   | 0
	1  0   | 0
	1  1   | 1



Вносим значения функции в клетки соответствующие входным наборам:

x2=0, x1=0 => 0

            x2
	 -------
          0   1
	+---+---+
    | 0 | 0 |   |
  x1|   +---+---+
    | 1 |   |   |
        +---+---+



x2=0, x1=1 => 0

            x2
	 -------
          0   1
	+---+---+
    | 0 | 0 |   |
  x1|   +---+---+
    | 1 | 0 |   |
        +---+---+



x2=1, x1=0 => 0

            x2
	 -------
          0   1
	+---+---+
    | 0 | 0 | 0 |
  x1|   +---+---+
    | 1 | 0 |   |
        +---+---+



x2=1, x1=1 => 1
            x2
	 -------
          0   1
	+---+---+
    | 0 | 0 | 0 |
  x1|   +---+---+
    | 1 | 0 | 1 |
        +---+---+

Все карта построенна.



  
  Пример заполнения (3 переменных) 
 

Попробуем теперь построить карту с 3 переменными.
Возьмем для этого функцию XOR.

Шаблон карты:

            0  x2   1
	 ------- -------	
	+---+---+---+---+
      0	|   |   |   |   |
    x1  +---+---+---+---+
      1 |   |   |   |   |
	+---+---+---+---+
	 --- ------- ---
          1     0     1  x3


Берем таблицу истинности:

	x3 x2 x1 | XOR
	---------+-----
	0  0  0  | 0
	0  0  1  | 1
        0  1  0  | 1
        0  1  1  | 0
        1  0  0  | 1
	1  0  1  | 0
	1  1  0  | 0
	1  1  1  | 1



Заполняем:
(0,0,0) => 0

            0  x2   1
	 ------- -------	
	+---+---+---+---+
      0	|   | 0 |   |   |
    x1  +---+---+---+---+
      1 |   |   |   |   |
	+---+---+---+---+
	 --- ------- ---
          1     0     1  x3



(0,0,1) => 1

            0  x2   1
	 ------- -------	
	+---+---+---+---+
      0	|   | 0 |   |   |
    x1  +---+---+---+---+
      1 |   | 1 |   |   |
	+---+---+---+---+
	 --- ------- ---
          1     0     1  x3



(0,1,0) => 1

            0  x2   1
	 ------- -------	
	+---+---+---+---+
      0	|   | 0 | 1 |   |
    x1  +---+---+---+---+
      1 |   | 1 |   |   |
	+---+---+---+---+
	 --- ------- ---
          1     0     1  x3



(0,1,1) => 0

            0  x2   1
	 ------- -------	
	+---+---+---+---+
      0	|   | 0 | 1 |   |
    x1  +---+---+---+---+
      1 |   | 1 | 0 |   |
	+---+---+---+---+
	 --- ------- ---
          1     0     1  x3



(1,0,0) => 1

            0  x2   1
	 ------- -------	
	+---+---+---+---+
      0	| 1 | 0 | 1 |   |
    x1  +---+---+---+---+
      1 |   | 1 | 0 |   |
	+---+---+---+---+
	 --- ------- ---
          1     0     1  x3



(1,0,1) => 0

            0  x2   1
	 ------- -------	
	+---+---+---+---+
      0	| 1 | 0 | 1 |   |
    x1  +---+---+---+---+
      1 | 0 | 1 | 0 |   |
	+---+---+---+---+
	 --- ------- ---
          1     0     1  x3



(1,1,0) => 0

            0  x2   1
	 ------- -------	
	+---+---+---+---+
      0	| 1 | 0 | 1 | 0 |
    x1  +---+---+---+---+
      1 | 0 | 1 | 0 |   |
	+---+---+---+---+
	 --- ------- ---
          1     0     1  x3



и наконец (1,1,1) => 1

            0  x2   1
	 ------- -------	
	+---+---+---+---+
      0	| 1 | 0 | 1 | 0 |
    x1  +---+---+---+---+
      1 | 0 | 1 | 0 | 1 |
	+---+---+---+---+
	 --- ------- ---
          1     0     1  x3

Карта готова



  
  Минтермы на Картах Карно 
 

Пример минтермов на карте Карно:
  

  


  



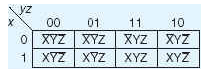
Примеры:

	   X2	                          X2 X3
	  0  1                          00 01 11 10     <---------------+
        +------+		      +-------------+	                |
X1    0	| 1  0 |                X1  0 |  0  0  1  0 |                   |
      1	| 0  0 |                    1 |  1  1  0  0 |                   |
        +------+                      +-------------+                   |
	                                                           --+  |
Обратите внимание что значения в строке/столбце меняются так, чтобы  |--+
изменялся один бит.                                                  |
                                                                   --+

	При числе переменных > 6, карты Карно становятся слишком
сложными для практического применения.



  
  Оптимизация с помощью карт Карно 
 

С помощью карт карно очень удобно выделять элементарные конъюнкции	

             X3X4
          00 01 11 10
    	+-------------+
      00|	      |		ячейка Z [X1,X2,X3,X4] = [0,1,1,1]
X1X2  01|       Z     |		Если она равна 1 то ей соответствует
      11|	      |		элементарная конъюнкция  где
      10|             |		если Xi == 1, то Xi
        +-------------+		ecли Xi == 0, то Xi#
                                т.e. для Z элементарная конъюнкция равна
					X1#*X2*X3*X4
			



Таким образом можно по карте Карно легко написать нормальную форму:

             X3X4
          00 01 11 10
    	+-------------+
      00| 1  0  0  0  |		F(X1,X2,X3,X4) = X1#*X2#*X3#*X4# +	
X1X2  01| 0  1  0  1  |                          X1#*X2*X3#*X4   +
      11| 0  0  0  1  |                          X1#*X2*X3*X4#   +
      10| 0  0  0  0  |                          X1*X2*X3*X4#
        +-------------+




Карта Карно помогает нам увидеть места где мы можем сократить ранг
элементарной конъюнкции (мв просто увидим соседние клетки):

             X3X4
          00 01 11 10
    	+-------------+
      00|	      |		
X1X2  01|       1  1  |		X1,X2,X3 у обоих клеток одинаковы
      11|	      |		X4 меняется - его можно выкинуть
      10|             |		Результат:  X1#*X2*X3 описывает обе клетки
        +-------------+




             X3X4
          00 01 11 10
    	+-------------+
      00|	      |		
X1X2  01|    1  1     |		X2 и X4 одинаковы, X1 и X3 меняются
      11|    1	1     |		Результат:  X2*X4
      10|             |
        +-------------+



На самом деле карта Карно является зацикленной с обоих сторон
(поэтому этот случай такой же кфк и предидущий):



		 +--------------+
                 |              |
                 V              |
             X3X4               |
          00 01 11 10           |
    	+-------------+         |    	X4 и X2 одинаковы, X1 и X3 меняются
      00| 1	    1 |		|	Результат:  X2#*X4#
X1X2  01|             |         |
 +--> 11|	      |<----+   |
 |    10| 1         1 |     |   |
 |      +-------------+     |   |
 |             ^            |   |
 |             |            |   |
 |             +------------|---+
 |			    |
 +--------------------------+





             X3X4
          00 01 11 10
    	+-------------+
      00|	1     |			X3 и X4 одинаковы, X1 и X2 меняются
X1X2  01|       1     |			результат:  X3*X4
      11|	1     |
      10|       1     |
        +-------------+





             X3X4
          00 01 11 10
    	+-------------+			X1 и X2 одинаковы, X3 и X4 меняются
      00|	      |			результат: X1#*X2
X1X2  01| 1  1  1  1  |
      11|	      |
      10|             |
        +-------------+





             X3X4
          00 01 11 10
    	+-------------+
      00| 1  1  1  1  |			X1 одинаковый, X2/X3/X4 меняются	
X1X2  01| 1  1  1  1  |			результат:  X1#
      11|	      |
      10|             |
        +-------------+





             X3X4
          00 01 11 10
    	+-------------+
      00|    1  1     |			X4 одинаковый, X1/X2/X3 меняются	
X1X2  01|    1  1     |			результат: X4
      11|    1	1     |
      10|    1  1     |
        +-------------+

 
Пример термов на карте карно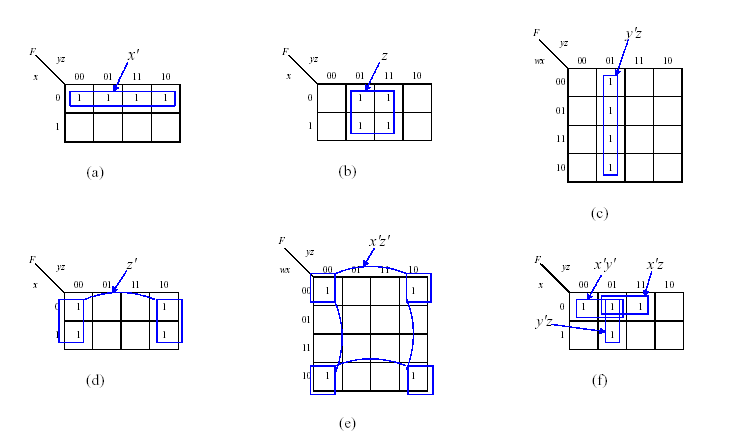 


  


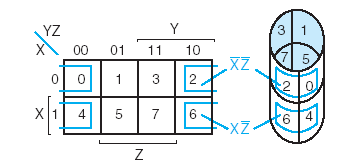
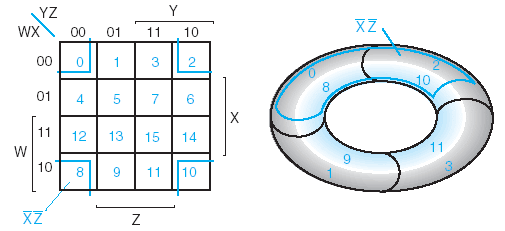
Связь карты карто и гиперкуба состояний:
  


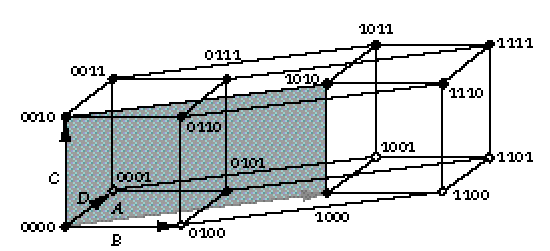
Минтермы соответствующего ранга - это вершины, ребра, грани, гиперграни гиперкуба.


  


  





  
  Оптимизация смежных конъюнкций 
 

Общая задача оптимизации - уменьшить число элементарных операций
для вычисления.


             X3X4
          00 01 11 10
    	+-------------+
      00|             |		Видим терм для оптимизации:
X1X2  01|   (1  1)    |         (X1,X2,X4 - одинаковые) => X1#*X2*X4 
      11|	1     | 	и отдельно [1111]	=> X1*X2*X3*X4
      10|             |
        +-------------+

т.e. функция F(x1,x2,x3,x4) = X1#*X2*X4 + X1*X2*X3*X4
	(одно сложение, 5 умножений),
но:

             X3X4
          00 01 11 10
    	+-------------+
      00|	^     |		
X1X2  01|    1  1     |		Можем описать вертикальный терм
      11|	1     |		(X2,X3,X4 - одинаковые => X2*X3*X4
      10|       V     |
        +-------------+

Поскольку 1 + 1 = 1, мы можем представить нашу функцию в виде перекрывания
термов:
          F(x1,x2,x3,x4) = X1#*X2*X4 + X2*X3*X4
	  (одно сложение, 4 умножения)



  
  Оптимизация при безразличных наборах 
 
Если у нас есть безразличные наборы мы можем трактовать их и как 0
и как 1 минимизируя функцию:



             X3X4
          00 01 11 10                             00 01 11 10
    	+-------------+                         +-------------+
      00|    X  1  1  |		              00|    0  1  1  |
X1X2  01|    X  1  X  |   трактуем как	      01|    0  1  1  |
      11|	1  X  |                       11|       1  1  |
      10|             |                       10|             |
        +-------------+                         +-------------+


Получаем 2 четверки:
	X1 и X3  постоянны     X1#*X3
	X2 и X3  постоянны     X2*X3

таким образом:  F(x1,x2,x3,x4) = X1#*X3 + X2*X3  	// 3 действия
дальнейшая оптимизация	       = X3 * (X1# + X2)	// 2 действия



  
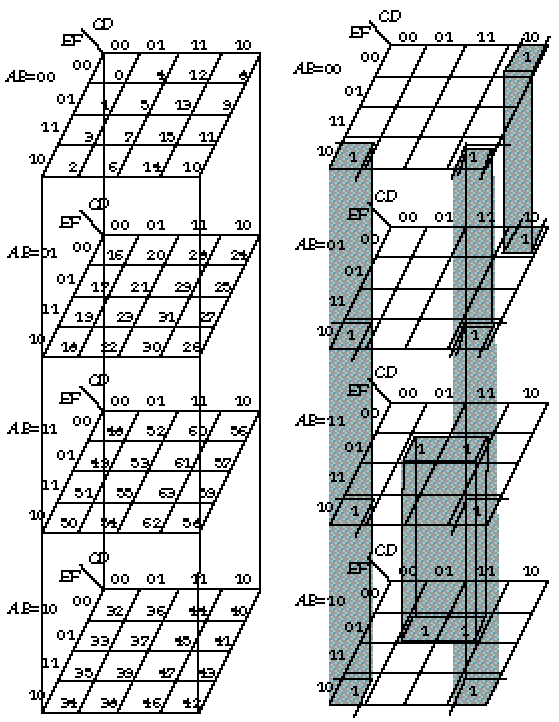
  Карты карно для большого числа переменных 
 

Карты карно для 5 переменных:

Как комбинация карт для 4х переменных


	     X5=0	    X5=1	
             X3X4            X3X4
          00 01 11 10     00 01 11 10
    	+-------------+ +-------------+
      00|    1        |	|    1        |		X1,X3,X4 - постоянны
X1X2  01|    1        | |    1        |         X2,X5    - меняются
      11|	      | |             |         Результат: X1#*X3#*X4
      10|             | |             |
        +-------------+ +-------------+

  


  




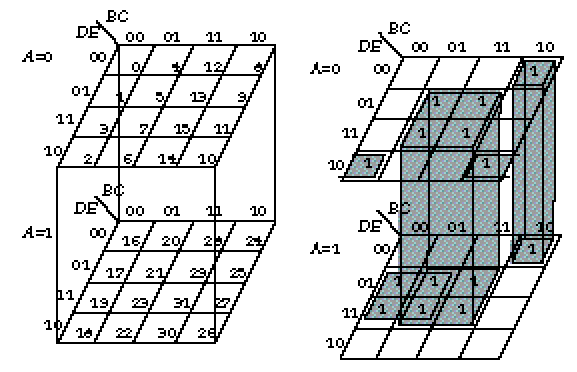
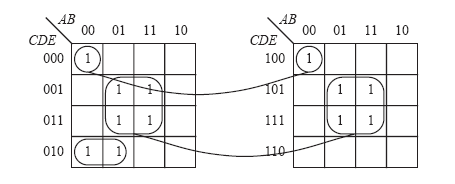
Карты Карно для 6 переменных


	     X5=0	    X5=1	
             X3X4            X3X4
          00 01 11 10     00 01 11 10
    	+-------------+ +-------------+
      00| 1           |	|             |	
X1X2  01|             | |             |   X6=0
      11|	      | |             |         X1,X2,X3,X4,X6 -постоянны	
      10|             | |             |		X6 - меняются
        +-------------+ +-------------+         Результат: 
    	+-------------+ +-------------+         X1#*X2#*X3#*X4#*X5#
      00| 1           |	|             |   X6=1
X1X2  01|             | |             |
      11|	      | |             |
      10|             | |             |
        +-------------+ +-------------+

  


  





  
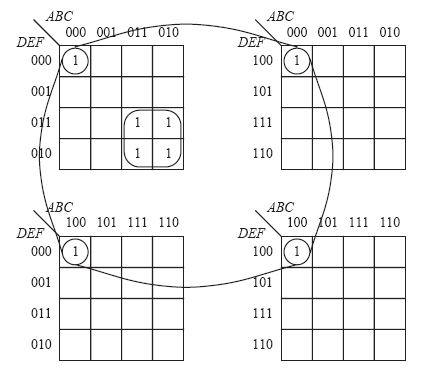
  Использование карт карно для макситермов 
 

           X2
	  0  1
	+------+
      0	| 0  1 |  
X1    1 | 1  0 |
	+------+

	F =  X1*X2# + X1#*X2 
	       10	01


смотрим не единицы а нули:

	F =  (X1 + X2) * (X1# + X2#)
		00	      11

       ----------------------------
       X1 X2   X1+X2	X1#+X2#	F
       ----------------------------
	00	0   	  1	0
	01      1         1     1
	10      1         1     1
	11      1         0     0
       ----------------------------

Вообще говоря при минимизации смотрят, что занимает меньшее количество
элементов (дизъюнктивная или конъюнктивная форма) и выбирают ее.

             X3X4
          00 01 11 10
    	+-------------+
      00| 1  1	1  1  |			X3 и X4 одинаковы, X1 и X2 меняются
X1X2  01| 1  0  1  1  |			результат:  X3*X4
      11| 1  1	1  1  |
      10| 1  1  1  0  |
        +-------------+

	F = (X1 + X2# + X3 + X4#) * (X1# + X2 + X3# + X4)

ясно что это меньше чем коньюктивная форма



  
  Оптимизация единичных 0 внутри блоков 1ц. 
 


             X3X4
          00 01 11 10
    	+-------------+
      00| 0  0	1  1  |		0 в блоке:
X1X2  01| 0  0  1  1  |		       	X1 = 1, X2 = 1, X4 = 1
      11| 0  0	0  1  |		
      10| 0  0  1  1  |
        +-------------+

Рассмотрим полный блок:

             X3X4
          00 01 11 10
    	+-------------+
      00| 0  0	1  1  |		
X1X2  01| 0  0  1  1  |		Полный блок X3			
      11| 0  0	1  1  |
      10| 0  0  1  1  |
        +-------------+


Результат для блока с нулем:

				X3 * (X1 * X2 * X4)#

				везде где X3 = 1,
				и где (X1,X2,X3) != (1,1,1)




             X3X4
          00 01 11 10
    	+-------------+
      00| 0  0	1  1  |		0 в блоке:
X1X2  01| 0  0  1  0  |		       	X1 = 0, X2 = 1, X4 = 0
      11| 0  0	1  1  |		
      10| 0  0  1  1  |
        +-------------+

Результат для блока с нулем:	X3 * (X1# * X2 * X4#)#



  
  A что если XOR? 
 


             X3X4
          00 01 11 10
    	+-------------+
      00| 0  1	0  1  |		
X1X2  01| 1  0  1  0  |	   XOR(x1,x2,x3,x4)	
      11| 0  1	0  1  |		
      10| 1  0  1  0  |
        +-------------+


             X3X4
          00 01 11 10
    	+-------------+
      00| 1  0	1  0  |		
X1X2  01| 0  1  0  1  |	   NOT(XOR(x1,x2,x3,x4))	
      11| 1  0	1  0  |		
      10| 0  1  0  1  |
        +-------------+


             X3X4
          00 01 11 10
    	+-------------+
      00| 1  0	1  0  |		
X1X2  01| 0  1  0  1  |	   тоже не подарок	
      11| 1  0	1  1  |		
      10| 0  1  1  1  |
        +-------------+


Собственно плохо оптимизируется как минтермами так и макстермами
Умение распозновать и использовать XOR - это исскуство :)