2.10. ТРОИЧНАЯ ЛОГИКА



Бывает логика более сложных порядков чем двоичная.






  
  Троичная логика 
 



Троичная логика
(Ternary logic)
мы смотрим сбалансированный вариант.
	---------------------------------------
	0	ложь		Minimal value
	i	фиг знает
	1	истина		maximum value
	---------------------------------------





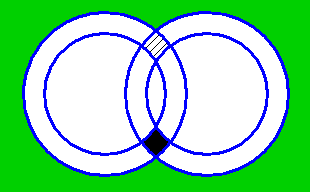
Расширенный вариант диаграммы Венна:

Для однооперандных функций:
Два вложенных круга, внутри внутреннего операнд = 1, между внешним и внутреннем
операнд = i, снаружи внешнего операнд = 0.
Значения:
	0	сплошной белый
	i	сплошной зеленый
	1	штрихованный черный

  


Для двухоперандных функций:

  

Два двойных круга и их пересечения.
Обратите внимание что зоне ii={A=i, B=i} соответсвуют два региона:
один выделен черным, другой зеленым.






  
  Однооперандные функции 
 



	---------------------------
	X	0	i	1
	---------------------------
		0	0	0	тождественный 0
		0	0	i	Сдвиг вниз (Shift down) (слабый == 1)
		0	0	1	Сильный == 1
		0	i	0	Слабый  == i
		0	i	i	Слабый  != 0
		0	i	1       повторение
		0	1	0	Сильный ==i
		0	1	i	Обмен i и 1    (Negation)
		0	1	1	Сильный != 0
		i	0	0	Слабый  == 0
		i	0	i	Слабый  != i
		i	0	1	Oбмен i и 0
		i	i	0	Слабый  != 1
		i	i	i    	тождественное i
		i	i	1
		i	1	0	Вращение вниз (Rotate down)
		i	1	i
		i	1	1	Сдвиг вверх (Shift Up)
		1	0	0	Cильный == 0
		1	0	i	Вращение вверх (Rotate up)
		1	0	1	Сильный != i
		1	i	0	инверсия (обмен 0 и 1)     	
		1	i	i
		1	i	1
		1	1	0	Сильный != 1
		1	1	i
		1	1	1	тождественная 1
	---------------------------








  
  NOT 
 


  



Отрицание:
	----------
	X	X#
	----------
	0	1
	i	i
	1	0
	----------
	-	+
	0	0
	+	-
	----------



  







  
  Shift Up 
 


  


	----------
	X       F	
	----------
	0	i
	i	1
	1	1
	----------
	-	0
	0	+
	+	+
	----------


  


	+---+
	| 1 |
	+---+
	  ^
	  |
	+---+
	| i |
	+---+
	  ^
	  |
	+---+
	| 0 |
	+---+






  
  Shift Down 
 


  


	----------
	X	F
	----------
	0	0
	i	0
	1	i
	----------
	-	-
	0	-
	+	0
	----------


  


	+---+
	| 1 |
	+---+
	  |
          V  
	+---+
	| i |
	+---+
	  |
	  V
	+---+
	| 0 |
	+---+








  
  Rotate Up 
 


  


	----------
	X       F	
	----------
	0	i
	i	1
	1	0
	----------
	-	0
	0	+
	+	-
	----------



  


           
	+---+
	| 1 |----+
	+---+    |
	  ^      |
	  |      |
	+---+    |
	| i |    |
	+---+    |
	  ^      |
	  |      |
	+---+    |
	| 0 |<---+
	+---+







  
  Rotate Down 
 


  


	----------
	X	F
	----------
	0	1
	i	0
	1	i
	----------
	-	+
	0	-
	+	0
	----------



  


           
	+---+
	| 1 |<---+
	+---+    |
	  |      |
	  v      |
	+---+    |
	| i |    |
	+---+    |
	  |      |
	  v      |
	+---+    |
	| 0 |----+
	+---+







  
  Сравнения 
 



X == A

Ecли X == A то результат 1 (если сильное сравнение), i (если слабое сравнение).
иначе 0.






Пример сильного сравнения == 1:

	----------
	X     ==1S	
	----------
	0       0
	i	0
	1	1
	----------
	-	-
	0	-
	+	+
	----------

	


  






Пример слабого сравнения == 1:
	----------
	X     ==1W	
	----------
	0       0
	i	0
	1	i
	----------
	-	-
	0	-
	+	0
	----------




  







Пример сильного сравнения <> 1:
	----------
	X     !=1S	
	----------
	0       1
	i	1
	1	0
	----------
	-	+
	0	+
	+	-
	----------


  






Пример слабого сравнения <> 1:
	----------
	X     !=1W	
	----------
	0       1
	i	1
	1	i
	----------
	-	+
	0	+
	+	0
	----------



  








  
  Некоторые двухоперандные функции 
 


В троичной логике только 729 коммутативных двухоперандных функций из 19,683
т.е. таких что F(A,B) = F(B,A)



  
  AND 
 


  


 X AND Y = MIN(X,Y)


  


	------------
	X  Y |	AND
	-----+------
	0  0 |  0
	0  i |  0
	0  1 |  0
	i  0 |  0
	i  i |  i
	i  1 |  i
	1  0 |  0
	1  i |  i
	1  1 |  1
	------------


	--+----------
	  | -  0  +
	--+----------
	- | -  -  -
	0 | -  0  0
	+ | -  0  +
	--+----------







  
  OR 
 


  


 X OR  Y = MAX(X,Y)


  


	------------
	X  Y |	OR
	-----+------
	0  0 |  0
	0  i |  i
	0  1 |  1
	i  0 |  i
	i  i |  i
	i  1 |  1
	1  0 |  1
	1  i |  1
	1  1 |  1
	------------


	--+----------
	  | -  0  +
	--+----------
	- | -  0  +
	0 | 0  0  +
	+ | +  +  +
	--+----------







  
  XOR 
 


Как вычислять логику более высшего порядка:

	Если при перемееном аргументе результат меняется (при его
изменении) то ставится неопределенное значение.

Пример вычислений XOR:

	XOR |  0  1		двоичный XOR
	----+-------
	  0 |  0  1
	  1 |  1  0


	----------------------------------------------
	AB        Local				Result
	----------------------------------------------
	00	0(+)0 = 0			0
	0i	0(+)0 = 0   0(+)1 = 1		i
	01	0(+)1 = 1			1
	i0	0(+)0 = 0   1(+)0 = 1		i
	ii	0(+)0 = 0   0(+)1 = 1  ... 
		1(+)0 = 1   1(+)1 = 0           i
	i1	0(+)1 = 1   1(+)1 = 0		i
	10	1(+)0 = 1			1
	1i	1(+)0 = 1   1(+)1 = 0		i
	11	1(+)1 = 0			0
	----------------------------------------------


Получаем результат:
	------------
	X  Y |	XOR
	-----+------
	0  0 |  0
	0  i |  i
	0  1 |  1
	i  0 |  i
	i  i |  i
	i  1 |  i
	1  0 |  1
	1  i |  i
	1  1 |  0
	------------

	XOR  |  0  i  1
	-----+-----------
	   0 |  0  i  1
	   i |  i  i  i
	   1 |  1  i  0


	--+----------
	  | -  0  +
	--+----------
	- | -  0  +
	0 | 0  0  0
	+ | +  0  -
	--+----------



  








  
  EQV 
 


	EQV(X,Y) = NOT (XOR(X,Y))

	------------
	X  Y |	EQV
	-----+------
	0  0 |  1		Экивалентен ли 0 - 0           : да
	0  i |  i		Экивалентен ли 0 - фиг знает   : фиг знает
	0  1 |  0
	i  0 |  i
	i  i |  i               Экивалентен ли Фиг знает - фиг знает : фиг знает
	i  1 |  i
	1  0 |  0
	1  i |  i
	1  1 |  1
	------------



	--+----------
	  | -  0  +
	--+----------
	- | +  0  -
	0 | 0  0  0
	+ | -  0  +
	--+----------



  







  
  NAND 
 


	NAND(X,Y) = NOT (AND(X,Y))

	------------
	X  Y |	NAND
	-----+------
	0  0 |  1
	0  i |  1
	0  1 |  1
	i  0 |  1
	i  i |  i
	i  1 |  i
	1  0 |  1
	1  i |  i
	1  1 |  0
	------------


	--+----------
	  | -  0  +
	--+----------
	- | +  +  +
	0 | +  0  0
	+ | +  0  -
	--+----------



  







  
  NOR 
 

	NOR(X,Y) = NOT((OR(X,Y))

	------------
	X  Y |	NOR
	-----+------
	0  0 |  1
	0  i |  i
	0  1 |  0
	i  0 |  i
	i  i |  i
	i  1 |  0
	1  0 |  0
	1  i |  0
	1  1 |  0
	------------



	--+----------
	  | -  0  +
	--+----------
	- | +  0  -
	0 | 0  0  -
	+ | -  -  -
	--+----------



  








  
  IMP 
 


Помним что функция несиммитричная

	------------
	X  Y |	X->Y
	-----+------
	0  0 |  1
	0  i |  1		0->0 = 1   0->1 = 1
	0  1 |  1
	i  0 |  i               0->0 = 1   1->0 = 0
	i  i |  i               0->0 = 1   0->1 = 1   1->0 = 0  1->1=1
	i  1 |  1		0->1 = 1   1->1 = 1
	1  0 |  0
	1  i |  i               1->0 = 0   1->1 = 1
	1  1 |  1
	------------



	--+----------
	  | -  0  +
	--+----------
	- | +  +  +
	0 | 0  0  0
	+ | -  0  +
	--+----------



  




А сейчас мы рассмотрим некоторые интерестные двухоперандные функции:






  
  Исключающий MAX 
 


  


XMAX:
	F = MAX(A,B), если A != B
	    0	    , если A == B
	(имейте в виду - это не XOR).

	  AB |  0   i   1
	-----+--------------
	   0 |  0   i   1
	   i |  i   0   1
	   1 |  1   1   0



	--+----------
	  | -  0  +
	--+----------
	- | -  0  +
	0 | 0  -  +
	+ | +  +  -
	--+----------



  







  
  Инверсно Исключающий MIN: 
 

IXMAX:

	F = MIN(A,B), если A != B
	    1	    , если A == B

	  AB |  0   i   1
	-----+--------------
	   0 |  1   0   0
           i |  0   1   i
           1 |  0   i   1 



	--+----------
	  | -  0  +
	--+----------
	- | +  -  -
	0 | -  +  0
	+ | -  0  +
	--+----------



  







  
  Mean 
 


  


Mean:
	Смотрит насколько "средние" операнды
	Если ii, то возращает 1
	Если iX или Xi, то возращает i
	Иначе 0

	  AB |  0  i   1
	-----+-------------
	   0 |  0  i   0
	   i |  i  1   i
	   1 |	0  i   0



	--+----------
	  | -  0  +
	--+----------
	- | -  0  -
	0 | 0  +  0
	+ | -  0  -
	--+----------



  








  
  Magnitude 
 


  

Magnitude:
	Сравнение 
	(Функция нессимитричная)
	Возращает 0, если A < B
		  i, если A = B
		  1, если A > B

	     |     B
	     | 0   i   1
	-----+-----------
	   0 | i   0   0
	A  i | 1   i   0
	   1 | 1   1   i	



	--+----------
	  | -  0  +
	--+----------
	- | 0  -  -
	0 | +  0  -
	+ | +  +  0
	--+----------



  








  
  Число логических функций 
 


Для двоичной системы счисления имеем:
	число однооперандных функций = 2^2 = 4
	число двухоперандных функций = 2^4 = 16


Для троичной системы счисления имеем:
	число однооперандных функций  = 3^3 = 27
	число двухоперандных функций  = посчитайте сами  (3^9)
	(ясное дело, что мы не будем здесь приводить эти функции).
	
	-----------------------------------------------------
	00  0i  01  i0  ii  i1  10  1i  11	входной набор
	-----------------------------------------------------
	cколько комбинаций? 3 для каждого значения входного
	набора, всего = 3^9 = 19683
	-----------------------------------------------------

	А вообще говоря число функций равно 3^(3^N), где N число аргументов
	для N=1  =                27
	для N=2  =            19,638
	для N=3  = 7,625,597,484,987 






  
  Трит и трайт 
 



трит	(0,i,1)
	единица информации - ячейка которая может быть в одном из трех состояний

  


	не стоит думать что
		1 трит  = 1.5 бита
	потому что:
		2 трита хранят = 3*3   = 9 комбинаций
		3 бита  хранят = 2*2*2 = 8 комбинаций
	т.е. 2 трита > 3 бита.

	На самом деле равные единицы информации - должны хранить равное число
	комбинаций.
	Имеем - есть некоторое число N:
		
		N = 2^m
		N = 3^k

		2^m = 3^k

	прологарифмируем по основанию e:

		m * ln 2 = k * ln 3

		     k * ln3
		m = ---------
		       ln 2
	                         1 * ln 3         1.098612
	соответсвенно 1 трит =  ---------- бит =  --------- бит = 1.5849 бит
	                          ln 2            0.693147
		
	соответсвенно 2 трита = 1.5849 * 2 = 3.1698 бит



трайт	(как правило 6 тритов).
	6 тритов могут хранить 3^6 = 729 состояний

	1 трайт = 1.5849 * 6 бит = 9.5094 бит = 9.5094 / 8 байт = 1.1887 байт






	3^1	3		
	3^2	9
	3^3	27
	3^4	81
	3^5	243
	3^6	729
	3^7	2187
	3^8	6561
	3^9	19683

	3^10	59049	





  
  Полиномальная форма 
 


Полиномальная форма троичных функций:

для функции с 1м переменным:

	F = A0 + A1*X + A2*X^2


для функции с 2мя переменными
	F = A0 + A1*X1 + A2*X2 + A3*X1^2 + A4*X2^2 + A5*X1*X2 +
      	       + A6*X1^2*X2 + A7*X1*X2^2 + A8*X1^2*X2^2

Полиномальная форма троичных функций очень важна практически, т.к.
элементы для оптических вычислений делают + и * на 3-ной ССОК.

	{0,1,2,...p-1}		p - основание системы счисления

	F(0) = c0
	F(1) = c1
	...
	F(p-1) = C{p-1}		в фигурных скобках индекс

	F(x) = SUM{I=0..p-1} (aI*x^I)  (mod p)

	c0 = a0
	c1 = a0 + a1 +... + a{p-1}
	c2 = a0 + 2*a1 + 2^2*a2+ .. + 2^(p-1)*a{p-1}
	....
	c{p-1} = a0 + (p-1)*a1 + (p-1)^2*s2 + ... + (p-1)^(p-1)a{p-1}

Для многовходовых:
	F(x,y) = fo(x) + f1(x)y + f2(x)*y^2 + ... + f{p-1}(x)*y^(p-1) (mod p)
	где
	fI(x) = a{0,i} + a{1,i}*x + a{2,i}*x^2 + .. + a{p-1,i}*x^(p-1)





Рассмотрим троичные функции с 1 переменной:

	F = A0 + A1*X + A2*X^2

	------------------------
			   X
	A2  A1  A0	0  1  2
	------------------------
	0   0   0	0  0  0
	0   0   1	1  1  1
	0   0   2	2  2  2
	0   1   0	0  1  2
	0   1   1	1  2  0
	0   1   2	2  0  1
	0   2   0	0  2  1
	0   2	1	1  0  2
	0   2   2	2  1  0
	1   0   0	0  1  1
	1   0   1	1  2  2
	1   0   2	2  0  0
	1   1   0	0  2  0
	1   1   1	1  0  1
	1   1   2	2  1  2
	1   2   0	0  0  2
	1   2   1	1  1  0
	1   2   2	2  2  1
	2   0   0	0  2  2
	2   0   1	1  0  0
	2   0   2	2  1  1
	2   1   0	0  0  1
	2   1   1	1  1  2
	2   1   2	2  2  0
	2   2   0	0  1  0
	2   2   1	1  2  1
	2   2   2	2  0  2
	------------------------

Как искать коэфициенты:

	F(0) = A0 + A1 * 0 + A2 * 0 = A0
	F(1) = A0 + A1     + A2     = A0 + A1 + A2
	F(2) = A0 + 2*A1   + A2     = A0 + 2*A1 + A2

пример:
	пусть F(0) = 1, F(1) = 2, F(2) = 1
	тогда
		A0 = 1

		A0 + A1 + A2 = 2
		1  + A1 + A2 = 2
		A1 + A2 = 1

		1  + 2*A1 + A2 = 1
		1  + A1 + (A1 + A2) = 1
		1  + A1 + 1 = 1
		A1 = -1		(т.е. 2)
		A1 = 2

		A1 + A2 = 1
		2  + A2 = 1
		A2 = -1		(т.е 2)
		A2 = 2


	---------------------------------------------------
			   X
	A2  A1  A0	0  1  2		Полином
	---------------------------------------------------
	0   0   0	0  0  0		0
	2   1   0	0  0  1         2x^2 + x
	1   2   0	0  0  2		x^2  + 2x
	2   2   0	0  1  0 	2x^2 + 2x
	1   0   0	0  1  1		x^2
	0   1   0	0  1  2		x
	1   1   0	0  2  0		x^2  + x
	0   2   0	0  2  1		2x
	2   0   0	0  2  2		2x^2
	2   0   1	1  0  0		2x^2 + 1
	1   1   1	1  0  1		x^2  + x + 1
	0   2	1	1  0  2		2x + 1
	1   2   1	1  1  0		x^2 + 2x + 1
	0   0   1	1  1  1		1
	2   1   1	1  1  2		2*x^2 + x + 1
	0   1   1	1  2  0		x + 1
	2   2   1	1  2  1		2*x^2 + 2x + 1
	1   0   1	1  2  2		x^2 + 1
	1   0   2	2  0  0         x^2 + 2
	0   1   2	2  0  1		x + 2
	2   2   2	2  0  2		2x^2 + 2x + 2
	0   2   2	2  1  0         2x + 2			NOT
	2   0   2	2  1  1		2x^2 + 2
	1   1   2	2  1  2		x^2 + x + 2
	2   1   2	2  2  0		2x^2 + x + 2
	1   2   2	2  2  1		x^2 + 2x + 2
	0   0   2	2  2  2		2
	---------------------------------------------------





как искать коэфициенты для троичной функции с 2 переменными:

	F(x,y) = A0 + A1*x  + A2*x^2   + A3*y      + A4*y^2 +
		    + A5*xy + A6*x^2*y + A7*x*y^2  + A8*x^2*y^2


F(0,0) = A0                  	определяем A0
F(1,0) = A0 + A1 + A2
F(2,0) = A0 + 2*A1 + A2		определяем A1,A2	
F(0,1) = A0 + A3 + A4
F(0,2) = A0 + 2*A3 + A4		определяем A3,A4

F(1,1) = A0 +   A1 + A2 +   A3 + A4 +   A5 +   A6 +   A7 + A8
F(2,1) = A0 + 2*A1 + A2 +   A3 + A4 + 2*A5 +   A6 + 2*A7 + A8
F(1,2) = A0 +   A1 + A2 + 2*A3 + A4 + 2*A5 + 2*A6 +   A7 + A8
F(2,2) = A0 + 2*A1 + A2 + 2*A3 + A4 +   A5 + 2*A6 + 2*A7 + A8

из последних 4 уравнений определяем A5,A6,A7,A8
 






  
  Базис 
 

Базис для троичной логики найти гораздо труднее.
Но существует функция которая является базисом в любой логике.
Это функция Уэбба

	W(X,Y) =  X + 1, если X == Y   
		  0    , если X != Y

		(X + 1 в арифметическом смысле)


Для двоичной системы это будет:
		----------
		XY      W
		----------
		00	1	зто будет NOR
		01      0
		10      0
		11      0
		----------


Для троичной системы:
		----------
		XY	W
		----------
		00	i
		0i      0
		01      0
		i0      0
		ii      1
		i1      0
		10      0
		1i      0
		11      0
		----------



	--+----------
	  | -  0  +
	--+----------
	- | 0  0  0 
	0 | 0  +  0
	+ | 0  0  -
	--+----------



  








  
  Арифметика 
 


В логическом смысле троичную логику мы рассмотрели
Теперь рассмотрим ее в арифметическом смысле:


	Цифра | Значение
	------+-------
	0     |  0
	1     |  i
	2     |  1


Имеем в виду, что у нас есть принципиально 2 арифметики
	троичная система  {0,1,2}
и	сбалансированная троичная система {-,0,+} = {-1,0,+1}
соответсвенно арифметические функции у этих систем принципиально разные


Полусумматор
На основании троичной логики можно строить троичные арифметические схемы
Например полусумматор (схема складывающая две цифры одного разряда):


	    |
	A+B |   0       1       2
	----+------------------------
	 0  |  00      01      02
	 1  |  01      02      10	старший бит - перенос
	 2  |  02      10      11	младший бит - сумма






Полусумматор: функция логической суммы:

	SUM |
	A+B |   0       1       2
	----+------------------------
	 0  |   0       1       2
	 1  |   1       2       0	
	 2  |   2       0       1	только младший бит - сумма


	SUM | 					
	A/B |	0	i	1               
	----+------------------------
	 0  |   0	i	1
	 i  |   i	1	0
	 1  |   1	0	i


	--+----------
	  | -  0  +
	--+----------   арифметика {0,1,2}
	- | -  0  +
	0 | 0  +  -
	+ | +  -  0
	--+----------


	--+----------
	  | -  0  +
	--+----------   арифметика {-,0,+}
	- | +  -  0
	0 | -  0  +
	+ | 0  +  -
	--+----------



  






Полусумматор: функция переноса:


	CARRY
	A+B |   0       1       2
	----+------------------------
	 0  |   0       0       0
	 1  |   0       0       1	только старший бит - перенос
	 2  |   0       1       1	

	CARRY					
	A/B |	0	i	1
	----+------------------------
	0   |   0	0	0
	i   |   0	0	i
	1   |   0 	i	i


	--+----------
	  | -  0  +
	--+----------  Арифметика {0,1,2}
	- | -  -  -
	0 | -  -  0
	+ | -  0  0
	--+----------


	--+----------
	  | -  0  +
	--+----------  Арифметика {-,0,+}
	- | -  0  0
	0 | 0  0  0
	+ | 0  0  +
	--+----------



  






Умножение:


Для {0,1,2}:

	A*B |   0       1       2
	----+------------------------
	 0  |   0       0       0
	 1  |   0       1       2	
	 2  |   0       2      11	


	MUL
	A*B |   0       1       2
	----+------------------------
	 0  |   0       0       0
	 1  |   0       1       2	только младший бит
	 2  |   0       2       1	


	CARRY					
	A*B |	0	i	1
	----+------------------------
	0   |   0	0	0
	i   |   0	0	0       только старший бит - перенос
	1   |   0 	0	1


Для {-,0,+} все сильно проще:
и никаких переносов.


  Умножение
	--+----------
	  | -  0  +
	--+----------
	- | +  0  -
	0 | 0  0  0
	+ | -  0  +
	--+----------
	









  
  Дополнительный код (троичный) 
 


Дополнительный код имеет смысл только для системы {0,1,2},
потому что система {-,0,+} может представлять отрицательные числа 
естественным способом.

Соответсвенно для {0,1,2} отрицательные числа удобно представлять 
в дополнительном коде (дополнение до 3)
тогда можно использовать сумматоры для вычитания:
	A - B = A + (-B)

-Х в дополнительном коде определяется как и в двоичном случае
(NOT(X) дополняет до 2, прибавлением единицы дополняем до 3)

	-X = NOT(X) + 1		в арифметическом смысле (1)
				т.е цифры:


Получаем функцию NEG (она же обмен i и 1):
(В двоичном случае - что NOT что NEG одинаковые, но в троичном они
 расслаиваются на две разные функции.

	X  | NEG
	---+----
	0  | 0
	i  | 1
	1  | i


  


Проверка:
	X + (-X) = 0

	X  -X | X + (-X)
	------+---------
	0  0  |   0
	i  1  |   0
	1  i  |   0

Все верно.

Особенно хочется обратить внимание что -X арифметическая функция и поэтому
она затрагивает все разряды числа:

Пример:
	Число    = 0i0
	NOT(1i)  = 1i1
	NEG(1i)  = 1i1 + 00i = 1i0 + 0i0 = 110
	             |     |          ^
	             +-----+          |
	                   |          |
	                   +----------+

	Проверка:  0i0 + 110 = 100 + i00 = (1)000






Законы троичной логики:


  






Расмотрим еще некоторые функции
{ -, 0, + }



  Сложение по модулю       
	--+----------
	  | -  0  +
	--+----------
	- | +  -  0
	0 | -  0  +
	+ | 0  +  -
	--+----------

  Перенос в сложении по модулю
	--+----------
	  | -  0  +
	--+----------
	- | -  0  0
	0 | 0  0  0
	+ | 0  0  +
	--+----------


  Сложение с насышением
	--+----------
	  | -  0  +
	--+----------
	- | -  -  0
	0 | -  0  +
	+ | 0  +  +
	--+----------


  Функция Webb
	--+----------
	  | -  0  +
	--+----------
	- | 0  +  -
	0 | +  +  -
	+ | -  -  -
	--+----------


   Тождество (строгоe)
	--+----------
	  | -  0  +
	--+----------
	- | +  -  -
	0 | -  +  -
	+ | -  -  +
	--+----------


   Тождество (weak)
	--+----------
	  | -  0  +
	--+----------
	- | +  0  -
	0 | 0  0  0      в общем как умножение
	+ | -  0  +
	--+----------


    Коньюнкция Лукашевича (сильная)
	--+----------
	  | -  0  +
	--+----------
	- | -  -  -
	0 | -  -  0
	+ | -  0  +
	--+----------


    Импликация Лукашевича
	--+----------
	  | -  0  +
	--+----------
	- | +  0  -
	0 | +  +  0
	+ | +  +  +
	--+----------

     Коньюнкция Клини
	--+----------
	  | -  0  +
	--+----------
	- | -  0  -
	0 | 0  0  0
	+ | -  0  +
	--+----------

     Импликация Клини 	
	--+----------
	  | -  0  +
	--+----------
	- | +  +  +
	0 | 0  0  0
	+ | -  0  +
	--+----------


     Интуиционистская импликация Геделя 
	--+----------
	  | -  0  +
	--+----------
	- | +  -  -
	0 | +  +  0
	+ | +  +  +
	--+----------

      Материальная импликация	
	--+----------
	  | -  0  +
	--+----------
	- | +  0  -
	0 | +  0  0
	+ | +  +  +
	--+----------


      Функция следования Брусенцова
	--+----------
	  | -  0  +
	--+----------
	- | +  0  -
	0 | 0  0  0
	+ | 0  0  +
	--+----------








  
  Info 
 



Webhttp://www.trinary.cc/Сайт посвященный разработке троичных устройств


SearchTrinary Logic
Index Prev Next