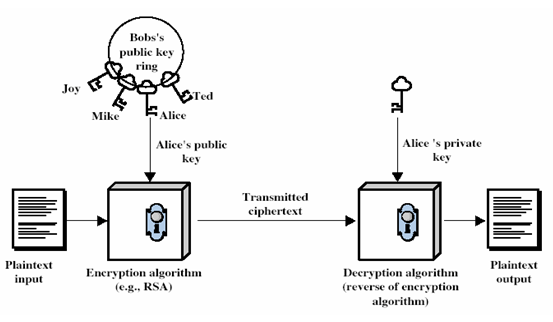
Аутефикация:
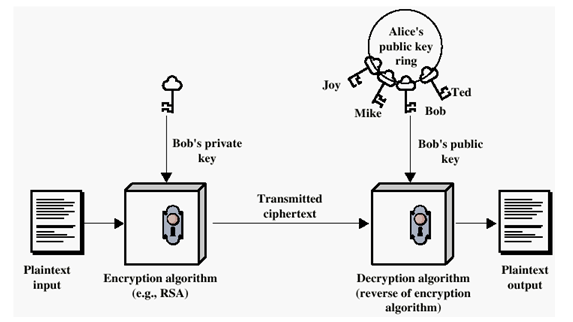
C открытым ключем: RSA C = M^e mod n M = C^d mod n = (M^e)^d mod n = M^(ed) mod n KU = {e,n} Открытый ключ (Unrestricted key) KR = {d,n} Закрытый ключ (Restricted key) p,q - два больших простых числа n = p * q e, gcd(F(n),e) = 1, 1 < e < F(n) F(n) - функция Эйлера (число положительнызх челых чисел меньших n, и взаимно простых с n. Для n = p*q, F(n) = (p-1)(q-1) d = e^(-1) mod F(n)
ECC (Elliptic Curve Cryptography)
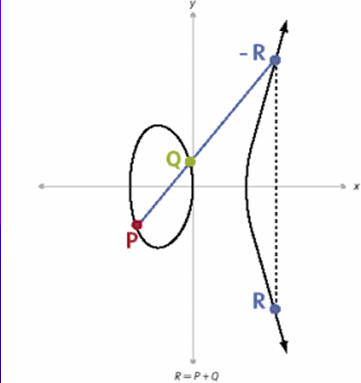
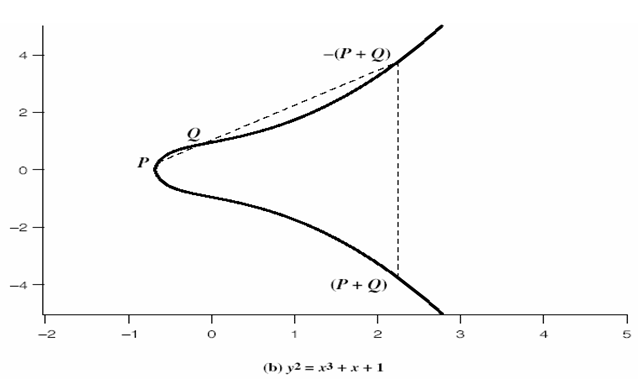
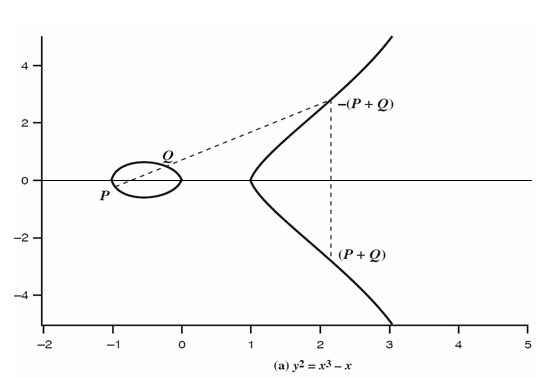
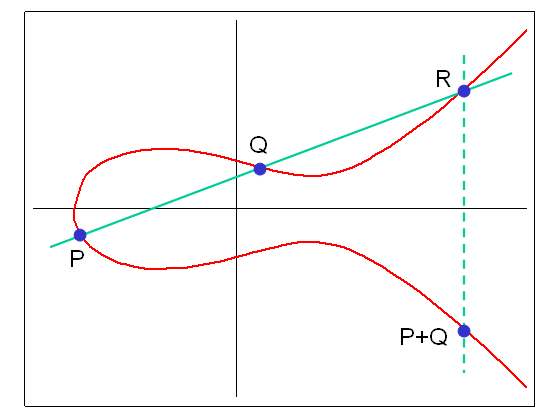
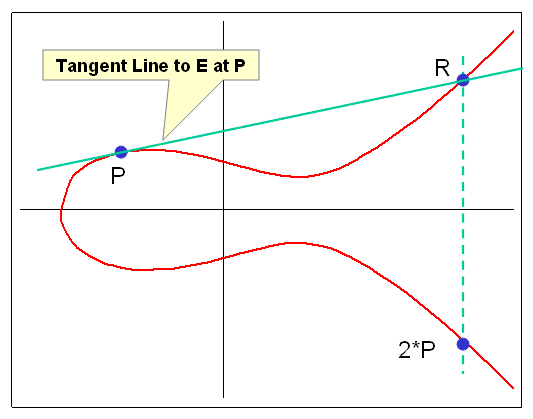
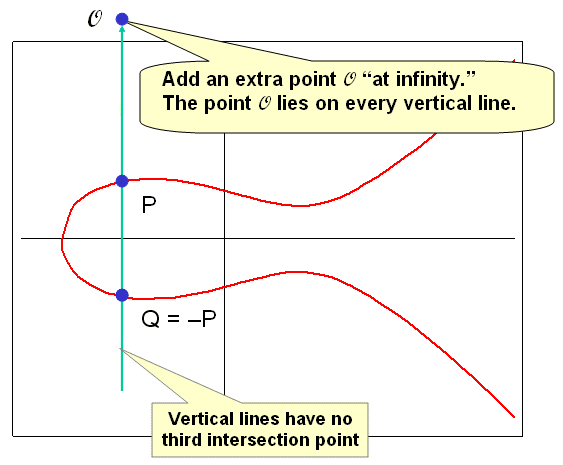
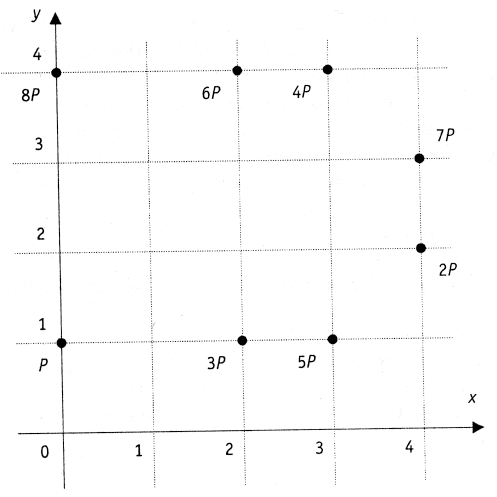
Пример эллиптической группы E(GF(5)), E: Y^2 = X^3 + X + 1 Точки: P (0,1) 2P (4,2) 3P (2,1) 4P (3,4) 5P (3,1) 6P (2,4) 7P (4,3) 8P (0,4) 9P O 10P = P
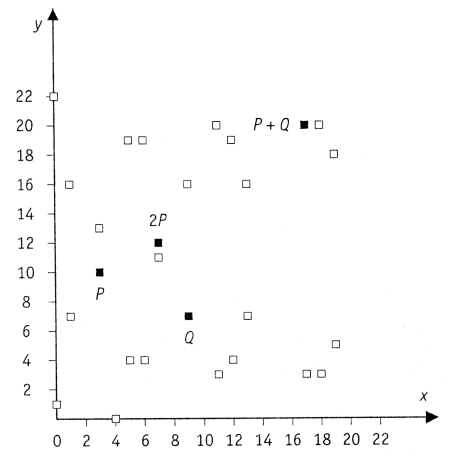
Пример эллиптической группы E(GF(23)), E: Y^2 = X^3 + X + 1 O (0,1) (0,22) (1,7) (1,16) (3,10) (3,13) (4,0) (5,4) (5,19) (6,4) (6,19) (7,11) (7,12) (9,7) (9,16) (11,3) (11,20) (12,4) (12,19) (13,7) (13,16) (17,3) (17,20) (18,3) (18,20) (19,5) (19,18)