THIS SECTION IS UNDER CONSTRUCTION
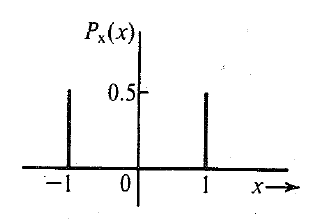


p(X) - вероятность события Х p(X,Y) - вероятнось и события Х и события Н p(X/Y) - условная веросяность вероятность события X, при условии что произошло событие Y 0 <= P(X) <= 1
P(A) = m/n _ P(A) = 1 - P(A) P(A+B) = P(A) + P(B) если несовместные P(A+B) = P(A) + P(B) - P(AB) если совместные P(AB) P(A/B) = --------- P(B) P(AB) = P(A) * P(B/A) P(AB) = P(B) * P(A/B) P(A) * P(B/A) P(A/B) = --------------- Теорема Байеса P(B) _ P(A\B) + P(A\B) = 1 P(AB) = P(A) * P(B) если события независимые
Монета (Coin) Орел (Heads) Решка (Tail) Какова вероятность что выпадут 3 орла подряд? P(H.H.H) = 1/2 * 1/2 * 1/2 = 1/8
Кость (Die) Какова вероятность что выбросим 12 очков? 6+6 P(12) = 1/6 * 1/6 = 1/36 Какова вероятность что выбросим 11 очков? P(11) = P(6+5) + P(5+6) = 2/36 Какова вероятность что выбросим 10 очков? случаи: 6+4 5+5 4+6 P(10) = 3 * 1/36 = 3/36 Какова вероятность что выбросим 9 очков? 6+3 5+4 4+5 3+6 а 8 очков: 6+2 5+3 4+4 2+6 3+5 7 очков: 6+1 5+2 4+3 3+4 2+5 1+6
Теперь проиллюстрируем на примере колоды карт: В колоде 52 карты 4 масти (Hearts = Червы, Diamons = Буби, Spides = Пики, Clubs = Трефы) в каждой масти 13 карт: A K Q J 10 9 8 7 6 5 4 3 2 (A = Ace = Туз) (K = King = Король) (Q = Queen = Дама) (J = Jack = Валет)
Вероятность вытащить из колоды Туза бубей

P(AD) = 1 / 52 (0.019)
Вероятность вытащить из колоды туза (неважно какой масти)

P(A) = P(AH) + P(AD) + P(AS) + P(AC) = 1/52 + 1/52 + 1/52 + 1/52 = 4/52 (0.077) другой спрсоб - нам подходят 4ре равновероятные карты.
Вероятность вытащить из колоды карту масти буби:

P(D) = 13 / 52 (0.25) (помним что в масти 13 карт)
Вероятность вытащить 2 красных туза P(AR.AR) = 2/52 * 1/51 = 2/2652 (0.00075)

есть только 2 варианта: XY AD потом AH 1/52 * 1/51 YX AH потом AD 1/52 * 1/51


Вероятность вытащить 2 туза P(A.A) = 4/52 * 3/51 = 12/2652 (0.0045)

варианты:

варианты: AH.AD AH.AS AH.AC AD.AH AD.AS AD.AC AS.AH AS.AD AS.AC AC.AH AC.AD AC.AS таким образом всего 12 вариантов
Вероятность вытащить точно одного туза из двух карт: P(A.X) = 2 * 4/52 * 48/51 = 384/2652 (0.144) Вариантов 2: AX или XA P(A.X) = 4/52 * 48/51 P(X.A) = 48/52 * 4/51


Вероятность вытащить хотя бы одного туза из двух карт Вариантов 2: A* и XA P = P(A*) + P(XA) P(A*) = 4/52 P(XA) = 48/52 * 4/51 P = 4/52 + 48/52 * 4/51 = (51 * 4 + 48 * 4) / 2652 = = 396 / 2652 (0.149)



Вероятность вытащить две карты масти Diamods P(D.D) = 13/52 * 12/51 = 156 /2652 (0.058) первую карту - 13 из 52 вторую карту - 12 из 51

Вероятность вытащить две карты одной масти Ecть 4 варианта: DD HH SS CC P = 4 * P(D.D) = 4* 13/52 * 12/52 = 624/2652 (0.235) И действительно возможные варианты: >DD< DH DS DC HD >HH< HS HC SD SH >SS< SC CD CH CS >CC< Вероятность должна быть немного меньше чем 1/4.
Вероятность вытащить точно два туза из трех карт. Ситуаций много: AAX AXA XAA вероятность для одного случая: AAX 4/52 * 3/51 * 48/50 AXA 4/52 * 48/51 * 3/50 XAA 48/52 * 4/51 * 3/50 P = 3 * 4/52 * 3/51 * 48/50 = 1728 / 132600 = (0.013)
Вероятность вытащить точно два туза из четырех карт: Ситуаций еще больше (комбинаторика рулит) AAXX AXAX AXXA XAAX XAXA XXAA Вероятность: P = 6 * 4/52 * 3/51 * 48/50 * 47/49
Роль информации в событии Кто-то говорит что у него двое детей и один из них мальчик Какова вероятность что у него два мальчика? Рассмотрим все возможные случаи с парами детей: MM MF FM FF (не вписывается в нашу задачу) Эти случаи равновероятны: Поэтому вероятность что у него 2 мальчика = 1/3 Кто-то говорит что у него двое детей и старший из них мальчик Какова вероятность что у него два мальчика? Рассмотрим все возможные случаи с парами детей: MM MF FM (не подходит) FF (не подходит) Поскольку случаи равновероятные То вероятность что у него 2 мальчика = 1/2
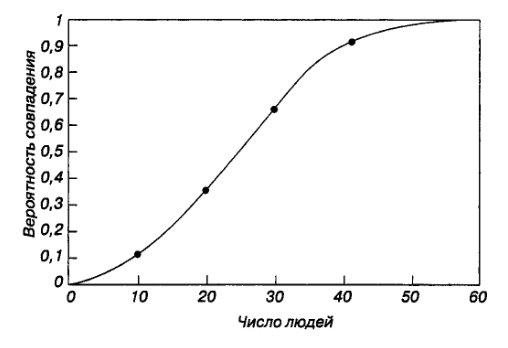
Парадокс дней рождений 2 человека - какова вероятность что день рождения совпадет? A-B 1/365 не совпадет 364/365 3 человека - какова вероятность что день рождения совпадет? A / \ B - C вероятность совпадения для каждой из пар = 1/365 таких пар = 3 Таким образом получаем ~3/365 более точные подсчеты: не совпадет 364 363 --- * --- 365 365 365*365 - 364*363 X^2 - (X-1)(X-2) = X^2 - X^2 + 3*X - 2 = 3*365-2 4 человека A - B | X | D - C всего 6 пар. Вероятность совпадения в паре = 1/365 6/365
THIS SECTION IS UNDER CONSTRUCTION
Понятно что у 366 человек - вероятность = 1
Корреляция: Удобно смотреть на графике: _ _ Y - Y от X - X
