3.17.3. ПОЛЯ ГАЛУА GF[p,k]
Поля Галуа существуют не только для GF[p] = GF[p,1], где p - простое число.
Но также для GF[p,k], где p - простое число, а k - целое число.
Только в случаях k > 1 мы работаем не с числами, а с полиномами.
(случай k = 1 - в общем то тоже полином, но вырожденный: 1).
GF[2^2]
GF[2^2] = GF[2,2] = GF[2, 2, X^2 + X + 1]
Элементы: { 0, 1, 2, 3 }
{ 00, 01, 10, 11 }
Сложение:
+ | 00 01 10 11
---+------------
00 | 00 01 10 11
01 | 01 00 11 10
10 | 10 11 00 01
11 | 11 10 01 00
Умножение:
примитивный полином: X^2 + X + 1 степени 2 [111]
представляем:
0 00
1=X^0 01
X 10
X^2 непредставим в сетке.
будем представлять по модулю образующего полинома:
X^2 100
X^2 + X + 1 111
----------- ---
X + 1 => 11
----------------------------------
X^inf 0 0 -
X^0 x^0 = 1 01 0
X^1 x^1 10 1
X^2 x^1 + 1 11 2
-----------------------------------
Логарифмы: { inf, 0, 1, 2 }
Тогда умножение в виде степеней
* | 0 1 2 3
---+----------
0 | - - - -
1 | - 0 1 2
2 | - 1 2 0
3 | - 2 0 1
реальная таблица умножения:
* | 1 2 3
---+--------
1 | 1 2 3
2 | 2 3 1
3 | 3 1 2
GF[2^3]
GF[2^3] = GF[2,3] = GF[2, 3, X^3 + X + 1]
Рассмотрим поле:
GF[8] = GF[2^3] = GF[2,3] = GF[2,3,X^2+X+1]
F(X) = u2 * x^2 + u1 * x + u0
где
u2,u1,u0 - элементы алгебраической системы S
Сложение:
по правилам для полиномов в классе вычетов 2:
+ | 000 001 010 011 100 101 110 111
---+--------------------------------
000| 000 001 010 011 100 101 110 111
001| 001 000 011 010 101 100 111 110
010| 010 011 000 001 110 111 100 101
011| 011 010 001 000 111 110 101 100
100| 100 101 110 111 000 001 010 011
101| 101 100 111 110 001 000 011 010
110| 110 111 100 101 010 011 000 001
111| 111 110 101 100 011 010 001 000
2+2 = 010 XOR 010 = 000 = 0 SUPER
а теперь в виде чисел:
+ | 0 1 2 3 4 5 6 7
--+-----------------
0 | 0 1 2 3 4 5 6 7
1 | 1 0 3 2 5 4 7 6
2 | 2 3 0 1 6 7 4 5
3 | 3 2 1 0 7 6 5 4
4 | 4 5 6 7 0 1 2 3
5 | 5 4 7 6 1 0 3 2
6 | 6 7 4 5 2 3 0 1
7 | 7 6 5 4 3 2 1 0
Умножение:
Что бы обеспечить умножение полиномов надо выбрать примитивный полином
соотвествующей степени. для нашего случая подходит X^3+X+1 [1011]
0 000 0 000
x^0 001 x^0 = 1 001
x^1 010 x 010
x^2 100 x^2 100
x^3 непредставим - берем по модулю примитивного полинома x^3 + X +1
x^3 1000
[1] x^3 + 0*X^2 + X + 1 1011
------------------------------------
X + 1 011
x^4 непредставим - берем по модулю
x^4 10000
[x] x^4 + 0*x^3 + X^2 + X 1011-
-----
110
x^5 непредставим - берем по модулю
x^5 100000
[x^2] x^5 + 0*x^4 + X^3 + X^2 1011--
------------------------ ------
x^3 + X^2 1100
[1] x^3 + 0 + X + 1 1011
----
111
x^6 непредставим - берем по модулю
x^6 1000000
[x^3] x^6 + 0 + X^4 + X^3 1011---
----------------------- -------
x^4 + X^3 11000
[x] x^4 + 0 + x^2 + X 1011-
------------------------------- ------
x^3+x^2+X 1110
X^3+0 +X + 1 1011
--------------- -------
x^2 + 1 101
----------------------------------------
power polynom vector regular
----------------------------------------
0 0 000 0
x^0=1 1 001 1
x^1 x 010 2
x^2 x^2 100 4
x^3 1+x 011 3
x^4 x+x^2 110 6
x^5 1+x+x^2 111 7
x^6 1+x^2 101 5
----------------------------------------
Соответственно степени
------------------------------------
Число log
------------------------------------
1 0 7 -7 -14
2 1 8 -6 -13
4 2 9 -5 -12
3 3 10 -4 -11
6 4 11 -3 -10
7 5 12 -2 -9
5 6 13 -1 -8
------------------------------------
таблица умножения в виде степеней
N| 1 2 3 4 5 6 7
--+---------------
N power | 0 1 3 2 6 4 5
---------+---------------
1 | 0| 0 1 3 2 6 4 5
2 | 1| 1 2 4 3 0 5 6
3 | 3| 3 4 6 5 2 0 1
4 | 2| 2 3 5 4 1 6 0
5 | 6| 6 0 2 1 5 3 4
6 | 4| 4 5 0 6 3 1 2
7 | 5| 5 6 1 0 4 2 3
а теперь в таблицу умножения
* | 1 2 3 4 5 6 7
---+---------------
1 | 1 2 3 4 5 6 7
2 | 2 4 6 3 1 7 5
3 | 3 6 5 7 4 1 2
4 | 4 3 7 6 2 5 1
5 | 5 1 4 2 7 3 6
6 | 6 7 1 5 3 2 4
7 | 7 5 2 1 6 4 3
2*2 = k^1 * k^1 = 4 (не всегда бывает так)
2*2 = k^(0-6) * k^(-6) = k(-12) = 4
Обратные элементы:
1 * 1 = 1
2 * 5 = 1
3 * 6 = 1
4 * 7 = 1
5 * 2 = 1
6 * 3 = 1
7 * 4 = 1
Индекс - показатель степени при X (по модулю примитивного полинома)
которое дает данный полином
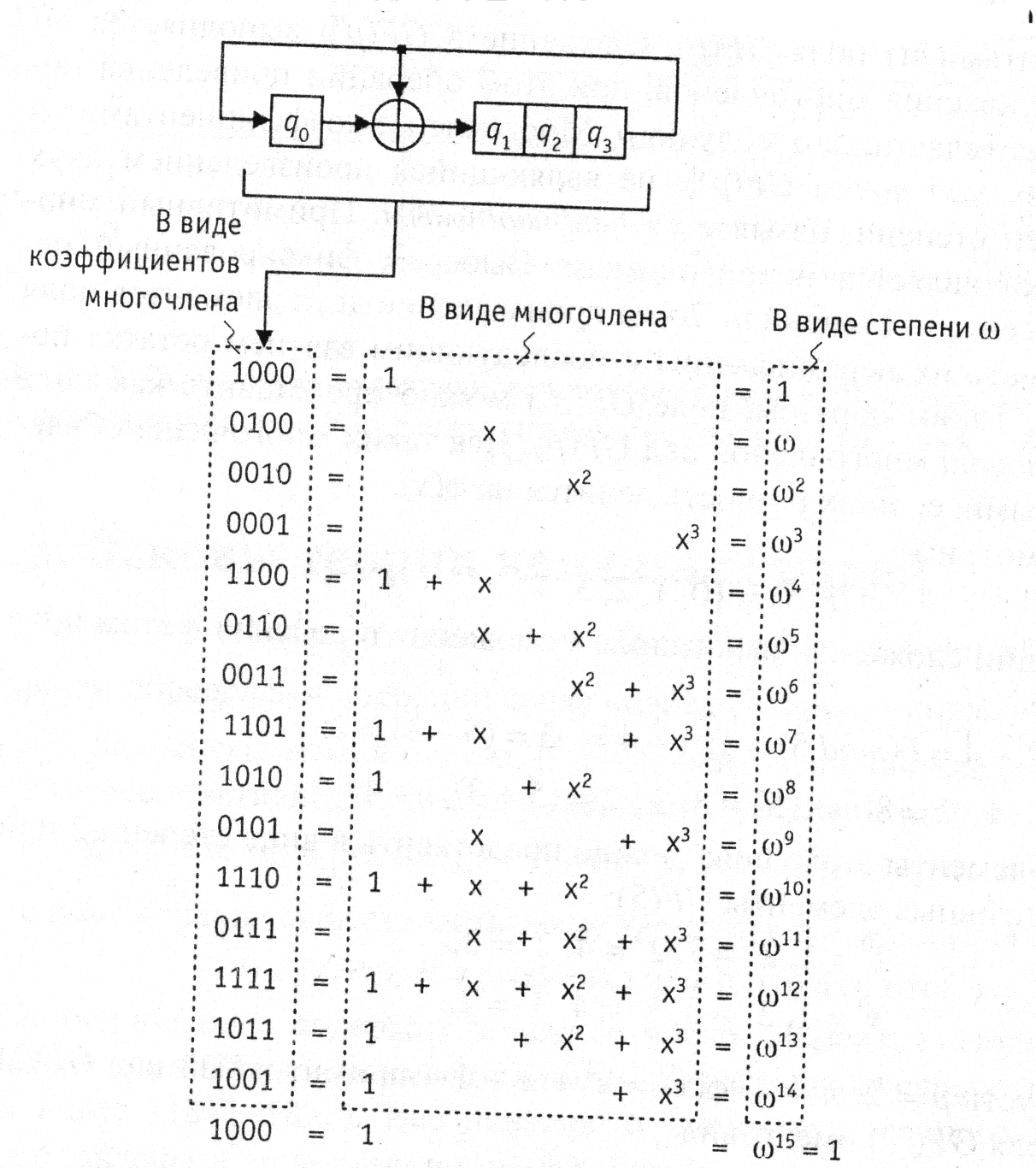
GF[2^4]
GF[3^2]
Рассмотрим теперь группу GF[3,2]:
GF[3^2] = GF[3,2] = GF[3,2, X^2 + 2X + 2]
сложение (обычное полиномальное по молулю 3):
+ | 00 01 02 10 11 12 20 21 22
---+----------------------------
00| 00 01 02 10 11 12 20 21 22
01| 01 02 00 11 12 10 21 22 20
02| 02 00 01 12 10 11 22 20 21
10| 10 11 12 20 21 22 00 01 02
11| 11 12 10 21 22 20 01 02 00
12| 12 10 11 22 20 21 02 00 01
20| 20 21 22 00 01 02 10 11 12
21| 21 22 20 01 02 00 11 12 10
22| 22 20 21 02 00 01 12 10 11
теперь переведем это в числа:
+| 0 1 2 3 4 5 6 7 8
--+--------------------
0| 0 1 2 3 4 5 6 7 8
1| 1 2 0 4 5 3 7 8 6
2| 2 0 1 5 3 4 8 6 7
3| 3 4 5 6 7 8 0 1 2
4| 4 5 3 7 8 6 1 2 0
5| 5 3 4 8 6 7 2 0 1
6| 6 7 8 0 1 2 3 4 5
7| 7 8 6 1 2 0 4 5 3
8| 6 7 6 2 0 1 5 3 4
Таблица умножения:
примитивный полином: X^2 + 2X + 2 [122]
Строим таблицу:
0 00
x^0=1 01
x^1 10
x^2 11
------------
100
122
---
11
x^3 21
------------
1000
122
110
122
---
21
x^4 02
-----------
10000
122
110
122
210 <-- обратите внимания все вычисления повторяются
211
---
02
x^5 20
----------
020
x^6 22
----------
200
211
---
22
x^7 12
----------
220
211
---
12
x^8 01 закончили
120
122
----
1
получаем:
---------------------------
Число Степень от 10
---------------------------
00 infinity
(1) 01 0 8 -8
(3) 10 1 9 -7
(4) 11 2 10 -6
(7) 21 3 11 -5
(2) 02 4 12 -4
(6) 20 5 13 -3
(8) 22 6 14 -2
(5) 12 7 15 -1
---------------------------
таблица умножения в виде степеней:
pow | 0 4 1 2 7 5 3 6
----+-----------------
0 | 0 4 1 2 7 5 3 6
4 | 4 0 5 6 3 1 7 2
1 | 1 5 2 3 0 6 4 7
2 | 2 6 3 4 1 7 5 0
7 | 7 3 0 1 6 4 2 5
5 | 5 1 6 7 4 2 0 3
3 | 3 7 4 5 2 0 6 1
6 | 6 2 7 0 5 3 1 4
таблица умножения в виде чисел:
* | 1 2 3 4 5 6 7 8
--+-----------------
1 | 1 2 3 4 5 6 7 8
2 | 2 1 6 8 7 3 5 4
3 | 3 6 4 7 1 8 2 5
4 | 4 8 7 2 3 5 6 1
5 | 5 7 1 3 8 2 4 6
6 | 6 3 8 5 2 4 1 7
7 | 7 5 2 6 4 1 8 3
8 | 8 4 5 1 6 7 3 2
2*2 = 1 SUPER
Обратные элементы:
1 * 1 = 1
2 * 2 = 1 <- обратите особое внимание
3 * 5 = 1
4 * 8 = 1
5 * 3 = 1
6 * 7 = 1
7 * 6 = 1
8 * 4 = 1
Кроме того модно просто умножать по модулю примитивного полинома
например
22 X^6
* 20 X^5
-----------------
110 результат обычного умножения полиномов
122 берем по модулю примитивного полинома
---
21 X^11 все правильно
Index Prev Next

