2.4. ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ

Идемпотентные законы:
еще их называют законами повторения или тавтологии.

	X + X  = X		
	X * X  = X




Комутативные (переместительные):
	
	X1 + X2	 = X2 + X1
	X1 * X2  = X2 * X1



Ассоциативные (сочетательные):

	X1 + X2 + X3 = X1 + (X2 + X3) = X2 + (X1 + X3) = X3 + (X1 + X2)
	X1 * X2 * X3 = X1 * (X2 * X3) = X2 * (X1 * X3) = X3 * (X1 * X2)



Дистрибутивные (распределительные):

	X1 * (X2 + X3)  =  X1 * X2  + X1 * X3  	конъюнкции относительно дизъюнкции
	X1 + X2 * X3	= (X1 + X2) * (X1 + X3) дизъюнкции относительно конъюнкции



Законы отрицания:

	0 + X  = X		
	0 * X  = 0

	1 + X  = 1	законы универсального множества			
	1 * X  = X

Законы дополнительности
	X + X# = 1	закон исключения третьего		
	X * X# = 0	закон логического противоречия



Закон двойного отрицания:
        _____   
          _     =
	( X ) = X = X



Законы Де-Моргана (Законы двойственности):

	_______   __   __
	X1 + X2 = X1 * X2

        _______   __   __
	X1 * X2 = X1 + X2

	в общей форме для N переменных
	(X1 + X2 + ... + XN)#  = X1# * X2# * ... * XN#
	(X1 * X2 + ... + XN)#  = X1# + X2# + ... + XN#



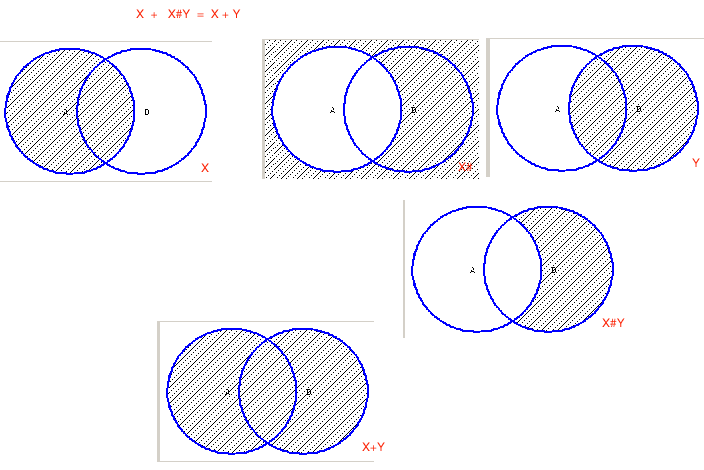
Законы поглощения (адсорбции):

	X + X * Y    = X
	X * (X + Y)  = X



Законы склеивания (распространения):
              _
	XY + XY = X
	        _
	(X+Y)(X+Y) = X



Законы обобщенного склеивания:

	     _              _
	XY + XZ + YZ = XY + XZ
	      _                   _
	(X+Y)(X+Z)(Y+Z) = (X + Y)(X + Z)

            _
	X + XY = X + Y
	  _
	X(X + Y) = XY




Законы связанные с XOR

собственно определение XOR:
	           _     _
	X (+) Y  = XY + XY  (по определению)

откуда:
	X (+) 0  = X
	X (+) 1  = X#
	X (+) X  = 0
	X (+) X# = 1

Комутативный:

	X (+) Y = Y (+) X

Ассоциативный:

	X (+) [Y (+) Z] = [X (+) Y] (+) Z

Дистрибутивный:
	X *   [Y (+) Z] = (X * Y) (+) (X * Z)


Следствия:

        _______   _ _         _               _
	X (+) Y = X*Y + X*Y = X (+) Y = X (+) Y

	            _
	X (+) XY = XY
	_     _    _   _
	X (+) XY = X * Y

	_          _
	X (+) XY = X + Y
	
	                _
	X (+) (X + Y) = XY
	_      _
	X (+) (X + Y) = XY
	       _        _   _
	X (+) (X + Y) = X + Y

	            _    _
	XY (+) (X + Y) = Y
	        _        _
        XY (+) (X + Y) = X
        _       _                     _               _
	XY (+) XY = XY (+) (X + Y) = (X + Y) (+) (X + Y) = X (+) Y

	_           _    ______          _
	XY (+) (X + Y) = X + Y# (+) (X + Y) = 1




Законы связанные с импликацией:

Закон контрапозиции:
                 _    _
	A -> B = B -> A

		 ______
	A -> B = A <- B

	         _
	A -> B = A + B	


	A ~ B = (A -> B) * (B -> A)



Все законы могут быть доказаны аналитически или перебором.

Пример доказательства аналитически:
              _
	XY + XY = X
	         _
	X * (Y + Y) = X		[ A*(B+C) = AB + AC ]
	                              _
	X * 1 = X,  		[ X + X = 1]

	X = X		тождество чтд


Пример доказательства перебором:

Надо доказать:
	X1 + X1 * X2 = X1

X1 может быть либо 0, либо 1.

Пусть X1=0, тогда
	0  + 0 * X2 = 0
	0  +   0    = 0
	0           = 0		тождество

Теперь пусть X1=1, тогда
	1 + 1 * X2  = 1
	1 + A       = 1
	1           = 1		тождество

Что и требовалось доказать.



Можно также доказывать теоретико-множественным методом: