11.4. СУММАТОР С УСКОРЕННЫМ ПЕРЕНОСОМ

  
  Ускоренный перенос 
 


В каскаде сумматоров перенос ползет от младшего бита к старшему.
Поэтому время выполнения сложения равно 
		T  = N * Ts
			N  - число бит
			Ts - задержка на однобитном сумматоре


Для этого примера мы полагаем что C0 = 0 (для простоты):


	       +-----+
	  A0  -| SUM |-- S0
	  B0  -|     |--+
	       +-----+  | C1
	    +-----------+ 
	    |  +-----+
	    +--| SUM |
	  A1  -|     |-- S1
	  B1  -|     |--+
	       +-----+  | C2
	    +-----------+ 
	    |  +-----+
	    +--| SUM |				T = 4 * Ts
	  A2  -|     |-- S2
	  B2  -|     |--+
	       +-----+  | C3
	    +-----------+ 
	    |  +-----+
	    +--| SUM |
	  A3  -|     |-- S3
	  B3  -|     |-- C4
	       +-----+  





Чтобы ускорить процесс сложения применяют схемы ускоренного переноса.
Ведь любой перенос от предидущего разряда можно выразить как логическую
функцию от переменных младших разрядов и время вычисления такой функции
будет меньше чем прохождение переноса через сумматор.


Для этого примера мы полагаем что C0 = 0 (для простоты):
		       +-----+
		  A0  -| SUM |-- S0
      +-----+	  B0  -|     |
      |     |	       |     |
A0 ---|	    |	       +-----+
B0 ---|	    |	       +-----+
      |Fast |	  A1  -| SUM |-- S1
A1 ---|Carry|	  B1  -|     |
B1 ---|	    |----------|     |			T = Tl + Ts
      |	    |	 C1    +-----+
A2 ---|	    |	       +-----+
A3 ---|	    |	  A2  -| SUM |-- S2
      +-----+	  B2  -|     |
       |   +-----------|     |
       |     C2	       +-----+
       |	       +-----+
       |	  A3  -| SUM |-- S3
       |	  B3  -|     |
       +---------------|     |-- C4
	  C3	       +-----+


Формула для ускоренного переноса

	C1 = A0*B0
	C2 = A1*B1 + A1*A0*B0 + B1*A0*B0
	C3 = A2*B2 + A2*A1*B1 + A2*A1*A0*B0 + A2*B1*A0*B0
		   + B2*A1*B1 + B2*A1*A0*B0 + B2*B1*A0*B0

	(собственно ускоренный перенос занимает 3-4 вентиля)

	но с ростом разрядности функция ускоренного переноса требует
все больше и больше места и Tl тоже растет.

Пример схемы сумматора с ускоренным переносом:
  





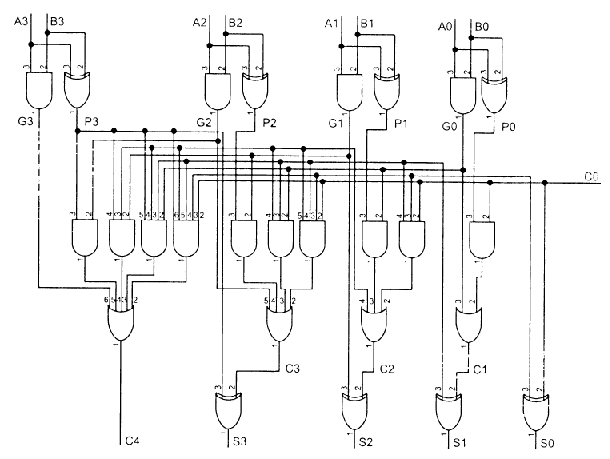
Реализация на Verilog:

	module fulladd4(sum,cout,a,b,cin);
		output	[3:0] sum;
		output	cout;
		input	[3:0] a,b;
		input	cin;

		wire	p0,g0,p1,g1,p2,g2,p3,g3;
		wire	c4,c3,c2,c1;

		assign	p0 = a[0] ^ b[0],
			p1 = a[1] ^ b[1],
			p2 = a[2] ^ b[2],
			p3 = a[3] ^ b[3];

		assign	g0 = a[0] & b[0],
			g1 = a[1] & b[1],
			g2 = a[2] & b[2],
			g3 = a[3] & b[3];

		assign  c1 = g0 | (p0 & cin),
			c2 = g1 | (p1 & g0) | (p1 & p0 & cin),
			c3 = g2 | (p2 & g1) | (p2 & p1 & p0 & cin),
			c4 = g3 | (p3 & g2) | (p3 & p2 & g1) | 
					      (p3 & p2 & p1 & g0) |
					      (p3 & p2 & p1 & p0 & cin);
		assign	sum[0] = p0 ^ cin,
			sum[1] = p1 ^ c1,
			sum[2] = p2 ^ c2,
			sum[3] = p3 ^ c3;

		assign	cout = c4;
	endmodule





С другой стороны при очень большой разрядности функции ускоренного переноса
получаются очень громоздкими (много места на кристалле), поэтому пользуются
комбинированными методами: сумматор делят на блоки с ускоренным переносом
(например по m бит [обычно по 4])


Для этого примера мы полагаем что C0 = 0 (для простоты):

		+------+
   	        | SUM4 |==== S3..S0
    A3..A0  ====| fast |
    B3..B0  ====|carry |---+
		+------+   |  C4
	     +-------------+	
	     |	+------+
   	     +--| SUM4 |==== S7..S4
    A7..A4  ====| fast |
    B7..B4  ====|carry |---+
		+------+   | C8
	     +-------------+	
	     |	+------+
   	     +--| SUM4 |==== S11..S8
   A11..A8  ====| fast |
   B11..B8  ====|carry |---+
		+------+   | C12
	     +-------------+
	     |	+------+
   	     +--| SUM4 |==== S15..S12
   A15..A12 ====| fast |
   B15..B12 ====|carry |---- C16
		+------+



	Время работы такого блока равно: Tl + Ts
	где  Tl - время работы схемы ускоренного переноса

	Полное же время работы сумматора в этом случае равно:

		T = (N / m) * (Ts + Tl)



Примем:
	N = 32
	m = 4
	Ts = Tl	(это почти верно)

	без ускоренного переноса:  T = 32 * Ts
	c ускоренным переносом:    T = (32 / 4) * (Ts + Tl)
				     = 8 * (Ts + Ts) = 16 * Ts
				   мы сократили время выполнения вдвое

Пример:
	N = 32
	m = 5
	Ts = Tl

	без ускоренного переноса:  T = 32 * Ts
	c ускоренным переносом:    T = (32 / 5) * (Ts + Tl)
				     = 7 * (Ts + Ts) = 14 * Ts



  
  Условный сумматор 
 

Как еще убыстрить схему:

	+------+
Axx   --| FAST |
Bxx   --|CARRY |------------+
	+------+            |
	                    |
	+------+            |
1   ----| SUM  |	 +-----+
Ai  ----|      |---------| MUX |
Bi  ----|      |         |     |
	+------+         |     |-------- Si
	                 |     |
	+------+         |     |
Ai  ----|HSUM  |---------|     |
Bi  ----|      |         +-----+
	+------+

Условный сумматор:
  


  


Время работы сумматора и Fast Carry логики примерно одинаковое.
Мы можем вычислить сумму в условии прихода переноса и в условии
его отсутствия, а паралельно рассчитать быстрый перенос. (Условный сумматор)
Затем просто выбрать правильный результат мультиплексором 2x1 (это быстро)

Cуммарно время выполнения уменьшается с Tl + Ts =~ 2Ts до max(Ts,Tl) + Tmux

		2Ts > Ts + Tmux

мы снова выиграли.

Пример 16-битного условного сумматора: 
  




  
  Сравнение сумматоров 
 

Сравнение сумматоров: