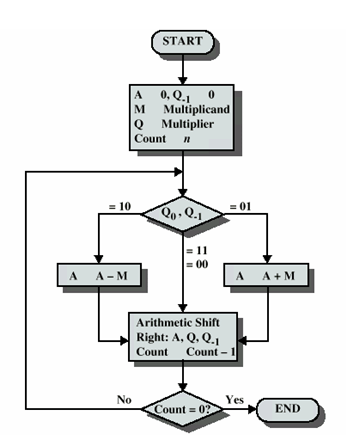
Алгоритм Бута:
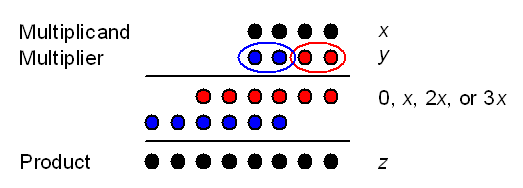
Простое умножение (для примера):
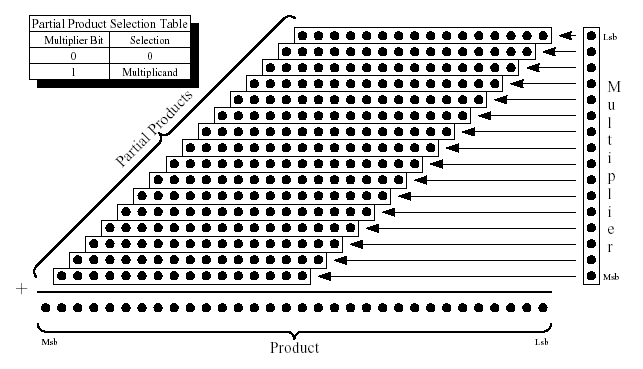
Простой умножитель Бута на 2 бита (MBR):
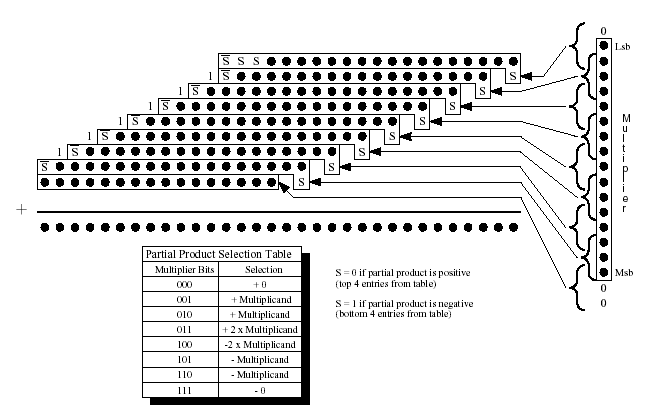
Схема ячейки в умножителе Бута
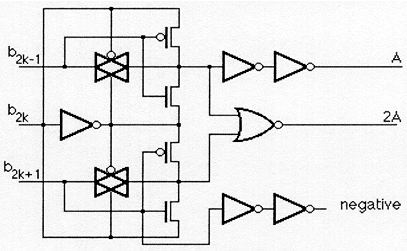
Топология ячейки в умножителе Бута

Умножитель Бута на 3 бита:
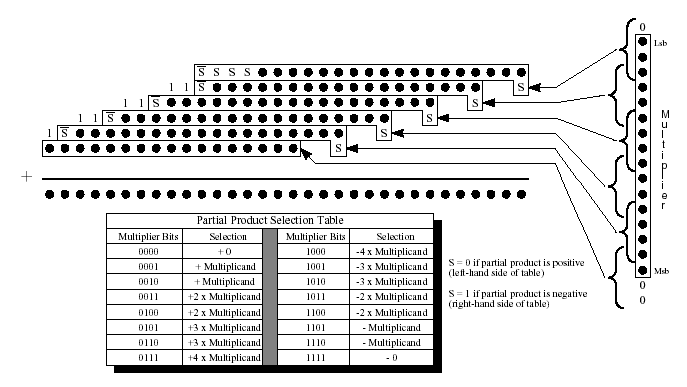
Метод Бута:
Идеи лежащие в основе семейства методов:
Общая идея:
Очевидно что:
2^m + 2^(2m-1) + ... + 2^k = 2^(m+1) - 2^k
Таким образом если мы найдем внутри множителя последовательность
единиц:
00011111000
то мы сможем ее заменить на
_
00100000100
уменьшив таким образом число частных произведений.
Метод Бута:
Берем множитель и анализируем ему 2 бита
(0,1) ------- > (-1, 0, 1)
(Для самого младшего разряда считаем что более младший разряд равен 0)
------------------------------------------------------------------
B{i}B{i-1} Что значит Что делаем
------------------------------------------------------------------
1 0 Начало цепочки из единиц вычитаем -M
0 1 Завершение цепочки из единиц прибавляем +M
0 0 нет цепочки единиц ничего не делаем
1 1 внутри цепочки единиц ничего не делаем
------------------------------------------------------------------
Модифицированный алгоритм Бута (MBR):
Анализируются сразу 3 разряда:
(0, 1) --- > (-2, -1, 0, -1, 2)
------------------------------------------------------------------
B{i+1}B{i}B{i-1} что значит что делаем
------------------------------------------------------------------
0 0 0 нет цепочки единиц ничего не делаем
0 0 1 завершение цепочки из единиц +M
0 1 0 одиноко стоящая единица +M
0 1 1 завершение цепочки единиц +2M
1 0 0 начало цепочки из единиц -2M
1 0 1 начало+завершение -M (-2M +M)
1 1 0 начало цепочки из единиц -M
1 1 1 внутри цепочки единиц ничего не делаем
------------------------------------------------------------------
Алгоритм Лемана:
Если две группы нулей разделены одной единицей то вместо вычитания
в позиции k и сложения в позиции (k+1) мы можем сделать сложение
в позиции k
k
|
000000100000
|
k+1
Если две группы единиц разделены нулем то вместо сложения в позиции
k и вычитания в позиции (k+1) можно сделать вычитание в позиции k
k
|
111110111111
|
k+1
Реализации:
умножение сразу на 2 бита.
минимизировать количество частных произведений
P = A * B = (a{n-1}*2^(n-1) + ... + a{0}*2^0) *
(b{n-1}*2^(n-1) + ... + b{0}*2^0) =
A*b{n-1}*2^(n-1)+ ... + A*b{0}*2^0
Заметим
b{i}*2^i = b{i}*2^(i+1) - 2*b{i}*2^(i-1)
Частные произведения после подстановки будут иметь вид
A * (-2*b{i+1} + b{i} + b{i-1}) * 2^i

Алгоритм Бута:

Простое умножение (для примера):

Простой умножитель Бута на 2 бита (MBR):

Схема ячейки в умножителе Бута

Топология ячейки в умножителе Бута

Умножитель Бута на 3 бита:
