14.2. МАТРИЧНЫЕ УМНОЖИТЕЛИ

	 C  S
         |  |
	 V  V
	+-----+
	| CPA | 	Carry Propagation Adder
	+-----+		Медленный T = ~ n*3L, где n-число разрядов
	   |
	   V
	   S

  





Простой матричный метод:


         A  B     C  D     E F
         |  |     |  |     | |
	 V  V     V  V     V V
	+-----+  +-----+  +-----+
	| CPA |  | CPA |  | CPA |
	+-----+  +-----+  +-----+
	   |	      |    |
	   |          V    V
     	   |	     +------+
	   |	     | CPA  |
	   |	     +------+
	   |	       |
	   +----+  +---+
		|  |
		V  V
	      +------+
	      | CPA  |
	      +------+
		 |
		 V

Время работы T = 9 nL



Умножение 5x5:
  




  
  Простой матричный умножитель 
 


Простой матричный умножитель:
  


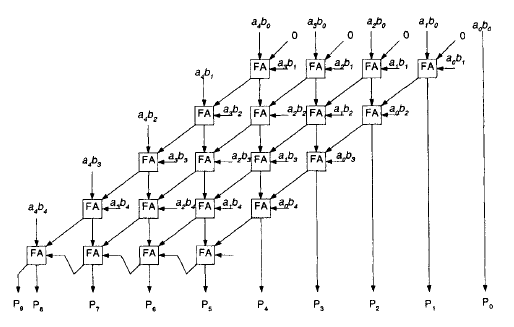
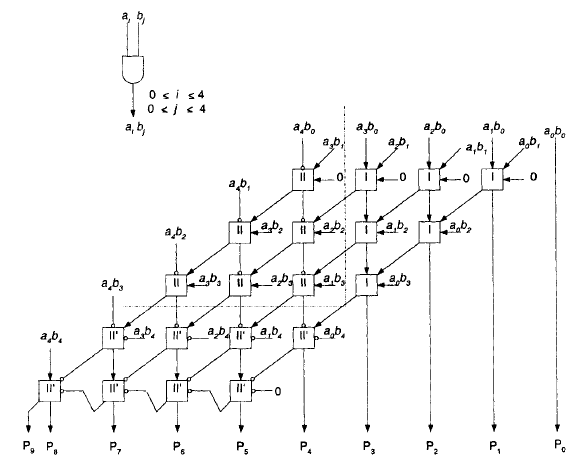
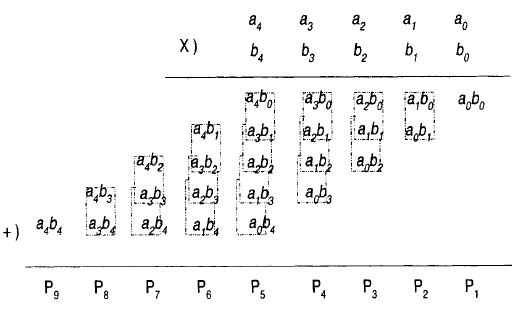
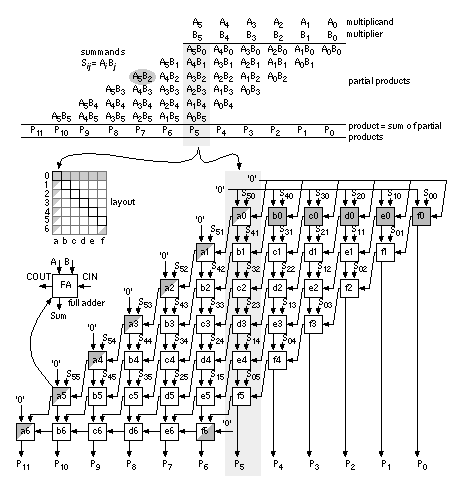
                     n-1  n-1
                     ---  ---
                     \    \   
	P = A * B =  /    /    A{i}B{j}*2^(i+j)
	             ---  ---
                     i=0  j=0



			A{n-1} ............ A{0}
			B{n-1} ............ B{0}
      ------------------------------------------
		        A{n-1}B{0}......A{0}B{0}		  
		       ....................
                      ....................
                     ....................
		    ...................
		   ..................
                 ..................
            A{n-1}B{n-1}..A{0}B{n-1}
      ------------------------------------------
     P{2n-1}  P{2n-2} ...................   P{0}



Простой матричный умножитель Брауна
(только положительные числа):
(использованы также полусумматоры, потому что верхняя строка все равно
складывает только 2 числа, а не 3 как остальные).
  


  


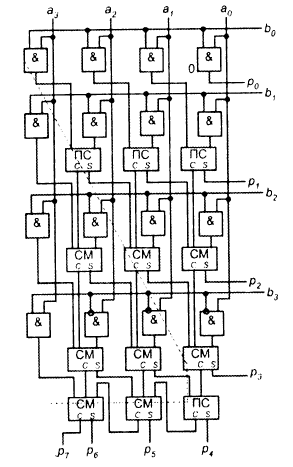
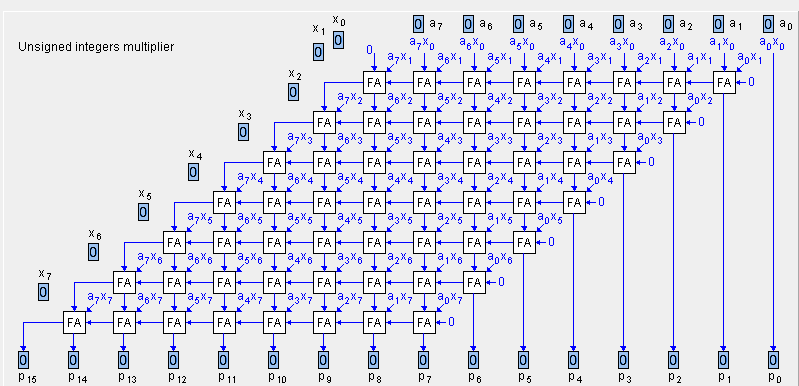
Беззнаковый простой матричный умножитель:
  


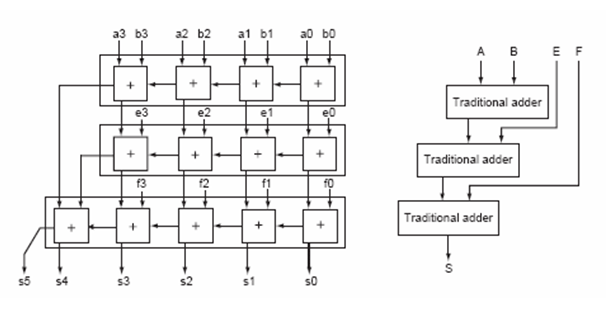
Число в дополнительном коде можно представить в виде:

                               n-2
			       ---	
	                       \
	X = -X{n-1}*2^(n-1) +  /   X{i}*(2^i)
	                       ---
			       i=0	


Поэтому если мы перемножим два числа в таком представлении и заменим у членов
знак минус на инверсию (для однобитового числа это одно и то же) то получим:


	P = A * B = A{n-1}B{n-1}*2^(2n-2)  +

                    n-2  n-2
	            ---  ---
		    \	 \   
		 +  /    /    A{i}B{j}*2^(i+j) +
		    ---  ---
		    i=0  j=0

		    n-2
		    ---
		    \   ___________
		 +  /   A{i}*B{n-1}*2^(i+n-1)  +
		    ---
		    i=0	

		    n-2
		    ---
		    \   ___________
		 +  /   A{n-1}*B{j}*2^(j+n-1) +
                    ---
                    j=0


		 + 2^n + 2^(2n-1)



Матричный умножитель в дополнительном коде:
  



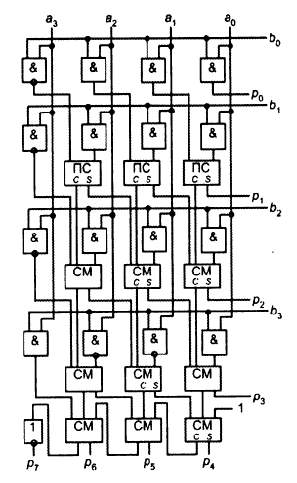
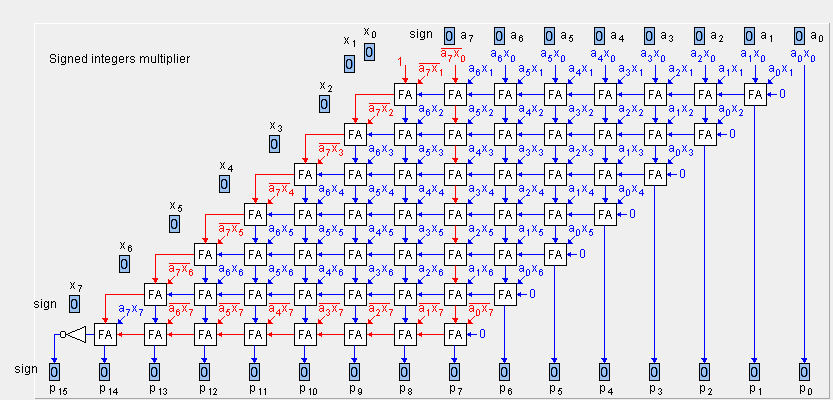
Знаковый простой матричный умножитель:
  





  
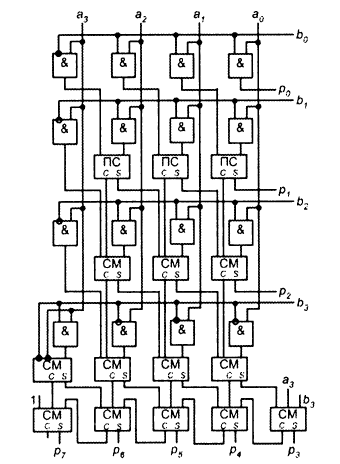
  Умножитель Бо-Вули 
 

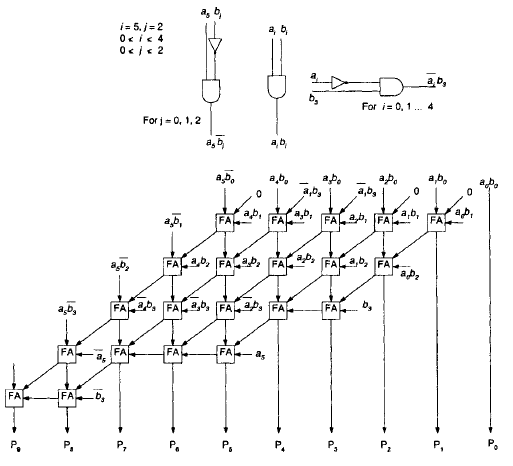
Умножитель Бо-Вули
(Baugh Wooley)

Матричный умножитель использующий немного другую схему для формирования
частичных произведений.

	                           ______   ______
	P = A * B = -(2^(2n-1)) + (A{n-1} + B{n-1} + A{n-1}B{n-1})*2^(2n-2) +

		    n-2  n-2
	            ---  ---
                    \    \
		  + /    /   A{i}B{j}*2^(i+j) +
		    ---  ---
		    i=0  j=0

		    n-2
		    ---
                    \   ____
		  + /   A{i}B{n-1}*2^(i+n-1)  +
		    ---
		    i=0

		    n-2
		    ---
		    \          ____
		  + /    A{n-1}B{j}*2^(j+n-1)  +
		    ---
		    j=0

		  + (A{n-1} + B{n-1})*2^(n-1)
		  
		 
Умножитель Бо-Вули:
  

  




  
  Умножитель Пезариса 
 

Умножитель Пезариса

(Pezaris)
Тоже матричный, но использует сумматоры четырех различных типов

Элементы применяемые в умножителе Пезариса:
  

  



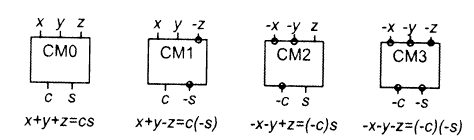
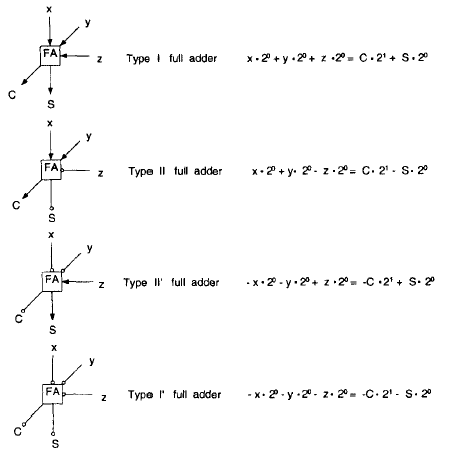
Умножитель Пезариса:
  

  



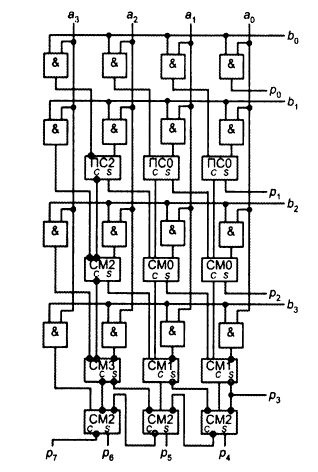
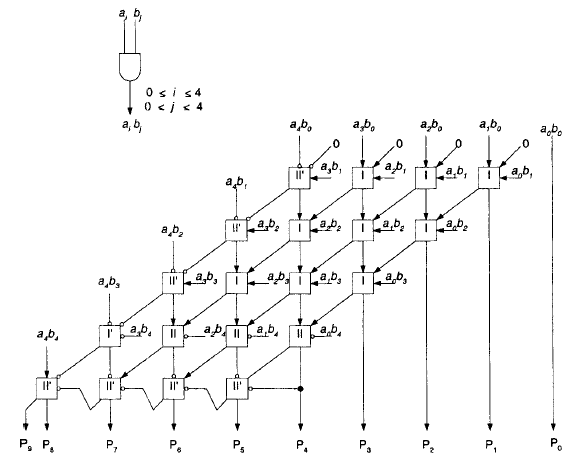
Двухсекционный умножитель:
  


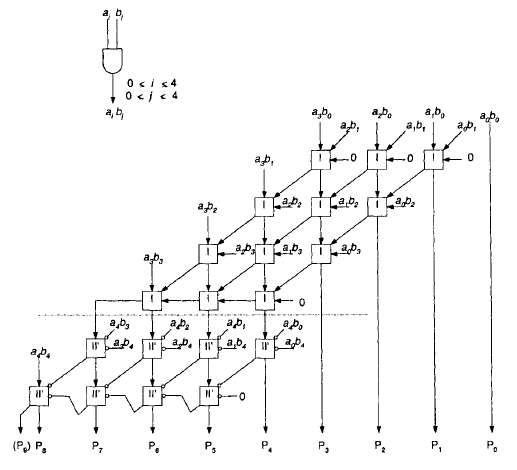
Трехсекционный умножитель: