Биномальные коэффициенты
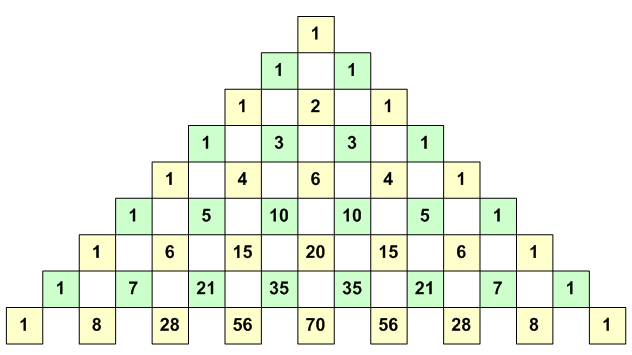
Треугольник Паскаля: n 1 0 1 1 1 1 2 1 2 1 3 3 1 3 1 4 6 4 1 4 1 5 10 10 5 1 5 1 6 15 20 15 6 1 6 1 7 21 35 35 21 7 1 7 1 8 28 56 70 56 28 8 1 8
Мультиномиальные коэффициенты:
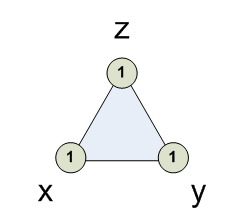
[1,0,0] = 1
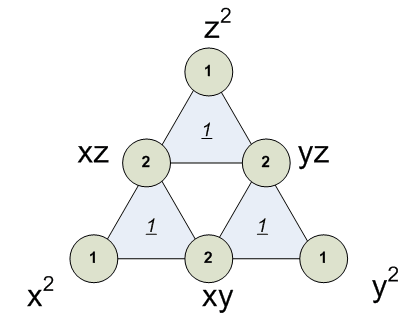
[2,0,0] = 1 [1,1,0] = 2
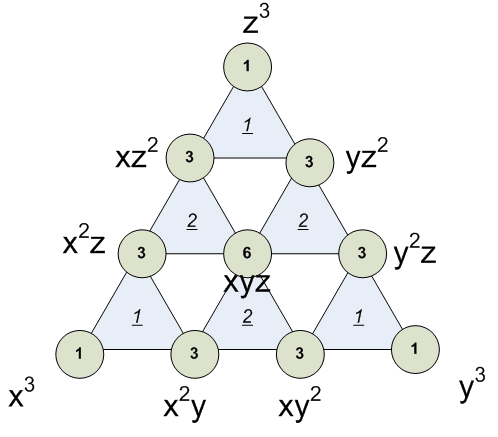
[3,0,0] = 1 [2,1,0] = 3 [1,1,1] = 6
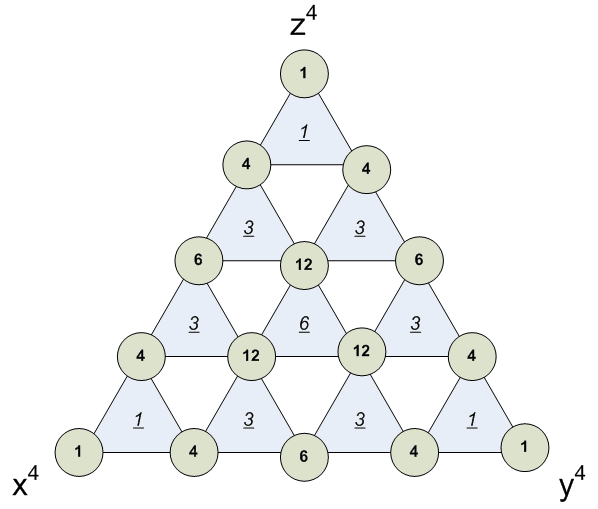
[4,0,0] = 1 [3,1,0] = 4 [2,2,0] = 6 [2,1,1] = 12
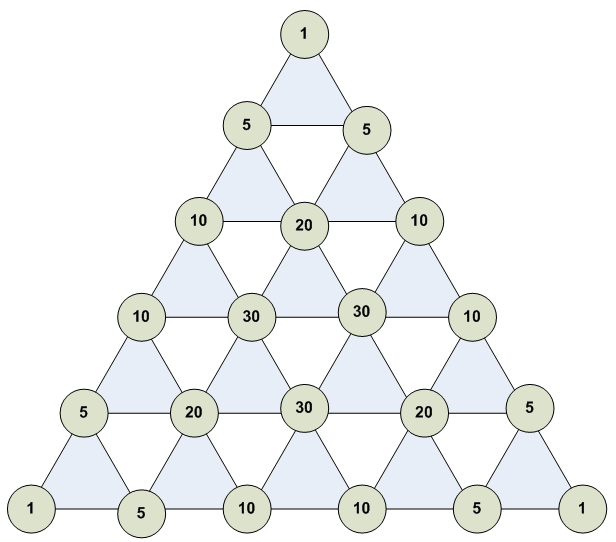
[5,0,0] = 1 [4,1,0] = 5 [3,2,0] = 10 [3,1,1] = 20 [2,2,1] = 30
[6,0,0] = 1 [5,1,0] = 6 [4,2,0] = 15 [4,1,1] = 30 [3,3,0] = 20 [3,2,1] = 60 [2,2,2] = 90
[7,0,0] = 1 [6,1,0] = 7 [5,2,0] = 21 [5,1,1] = 42 [4,3,0] = 35 [4,2,1] = 105 [3,3,1] = 140
Для четырех переменных:
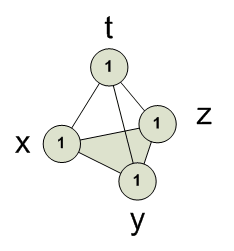
[1,0,0,0] = 1
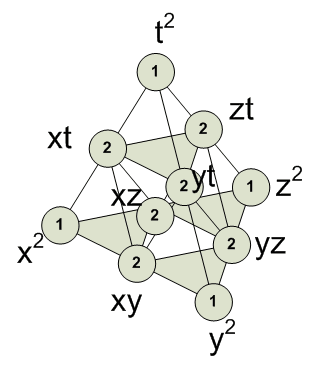
[2,0,0,0] = 1 [1,1,0,0] = 2
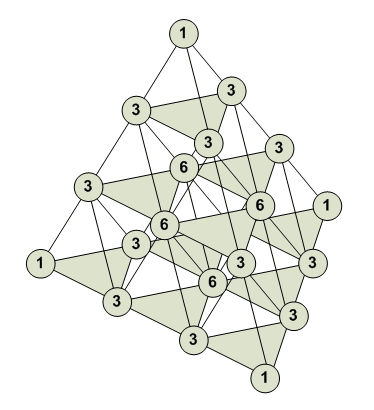
[3,0,0,0] = 1 [2,1,0,0] = 3 [1,1,1,0] = 6
[4,0,0,0] = 1 [3,1,0,0] = 4 [2,2,0,0] = 6 [2,1,1,0] = 12 [1,1,1,1] = 24
[5,0,0,0] = 1 [4,1,0,0] = 5 [3,2,0,0] = 10 [3,1,1,0] = 20 [2,2,1,0] = 30 [2,1,1,1] = 60
[6,0,0,0] = 1 [5,1,0,0] = 6 [4,2,0,0] = 15 [4,1,1,0] = 30 [3,3,0,0] = 20 [3,2,1,0] = 60 [3,1,1,1] = 120 [2,2,2,0] = 90 [2,2,1,1] = 180
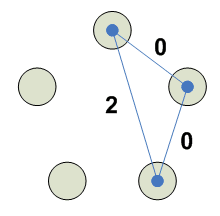
Сочетания
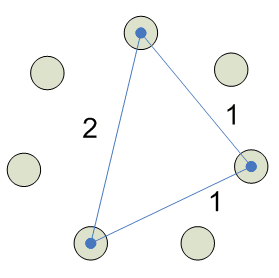
2
3
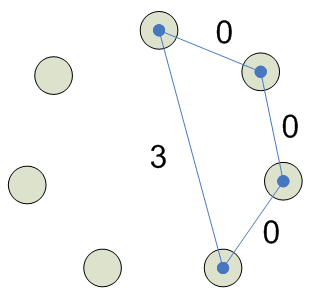
4
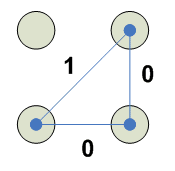
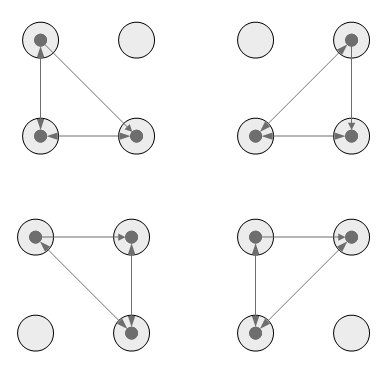
5
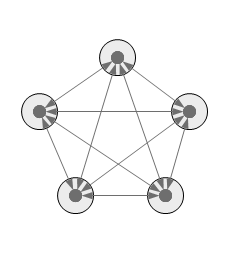
6
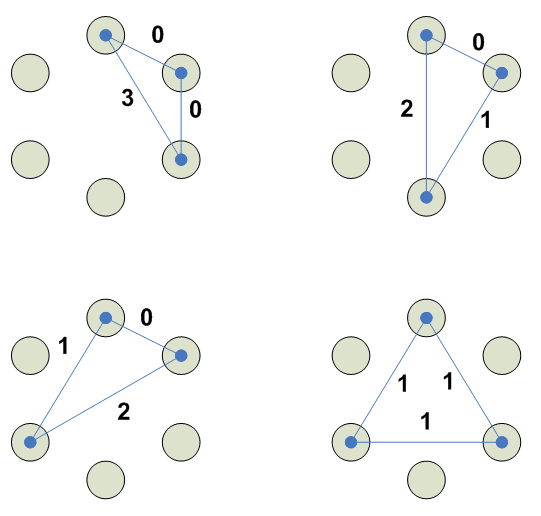
7
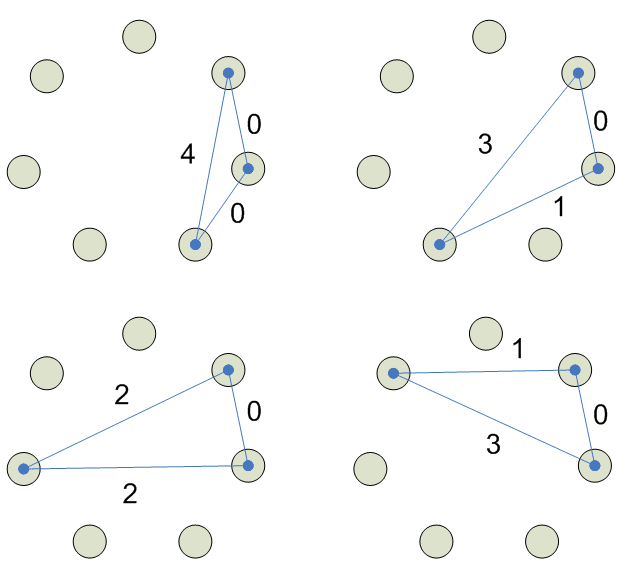
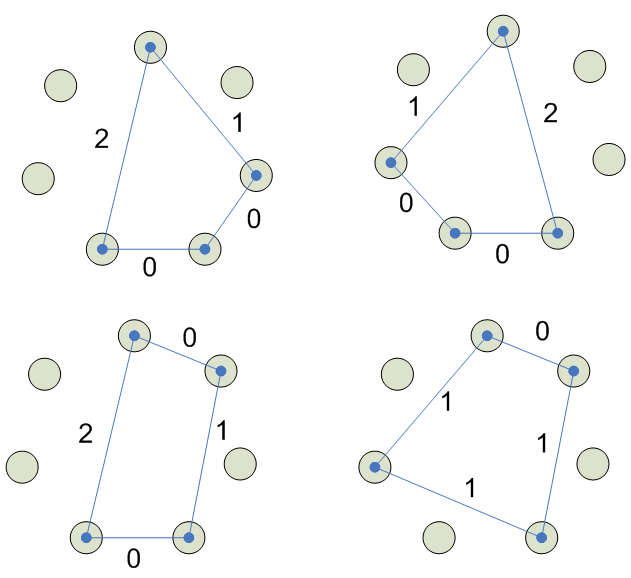
8
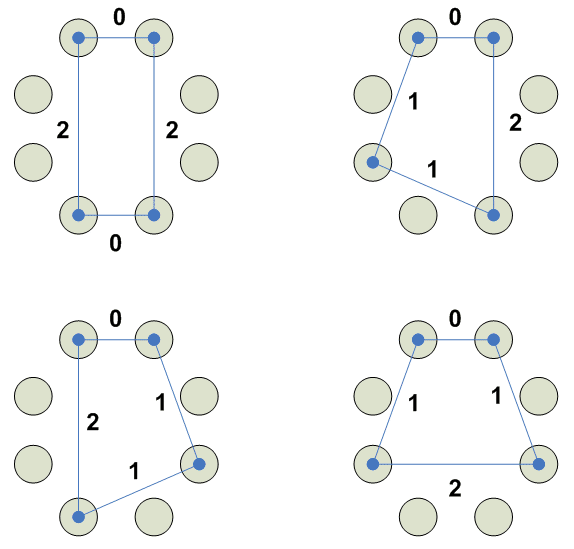
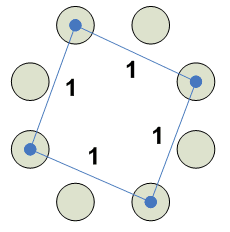
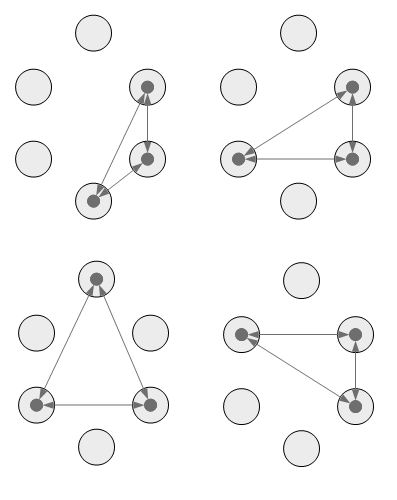
Каким образом считать двойные сочетания.
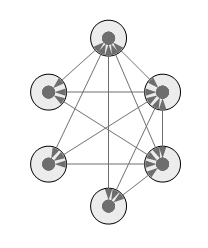

Но для каждой уникальной перестановки возможно 2^R вариантов Минтермов. примеры: ------------------------------------------------------ 2 3 2 3 ранг минтерма XX- X-XX X--X X--X-X- перестановка ------------------------------------------------------ 00- 0-00 0--0 0--0-0- варианты 01- 0-01 0--1 0--0-1- 10- 0-10 1--0 0--1-0- 11- 0-11 1--1 0--1-1- 1-00 1--0-0- 1-01 1--0-1- 1-10 1--1-0- 1-11 1--1-1- ------------------------------------------------------ Таким образом: Количество переменных = N Количество минтермов ранга R = С(N,R) * 2^R Пример для N=3 ранга 3: 1 * 2^3 = 1 * 8 = 8 ранга 2: 3 * 2^2 = 3 * 4 = 12 ранга 1: 3 * 2^1 = 3 * 2 = 6 ранга 0: 1 * 2^0 = 1 * 1 = 1 Например для N=4: ранга 4: 1 * 2^4 = 1 * 16 = 16 ранга 3: 4 * 2^3 = 4 * 8 = 32 ранга 2: 6 * 2^2 = 6 * 4 = 24 ранга 1: 4 * 2^1 = 4 * 2 = 8 ранга 0: 1 * 2^0 = 1 * 1 = 1 Пример для N=5 ранга 5: 1 * 2^5 = 1 * 32 = 32 ранга 4: 5 * 2^4 = 5 * 16 = 80 ранга 3: 10 * 2^3 = 10 * 8 = 80 ранга 2: 10 * 2^2 = 10 * 4 = 40 ранга 1: 5 * 2^1 = 5 * 2 = 10 ранга 0: 1 * 2^0 = 1 * 1 = 1 Для N=6: ранга 6: 1 * 2^6 = 1 * 64 = 64 ранга 5: 6 * 2^5 = 6 * 32 = 192 ранга 4: 15 * 2^4 = 15 * 16 = 240 ранга 3: 20 * 2^3 = 20 * 8 = 160 ранга 2: 15 * 2^2 = 15 * 4 = 60 ранга 1: 6 * 2^1 = 6 * 2 = 12 ранга 0: 1 * 2^0 = 1 * 1 = 1
Геометрический смысл биномальных коэффициентов
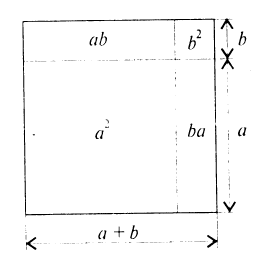
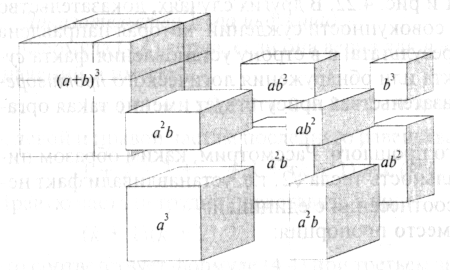
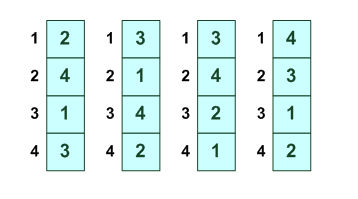
Перестановки
1

----- 1 1 -----
2
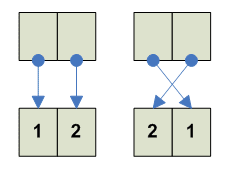
e: --------- 1 2 1 2 ---------
--------- 1 2 2 1 ---------
3
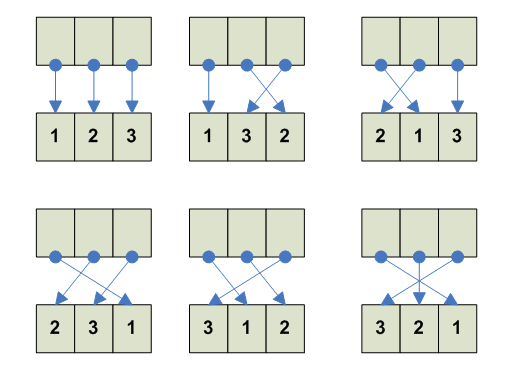
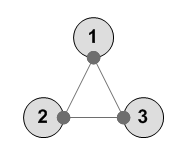
---------- 1 2 3 1 2 3 ---------
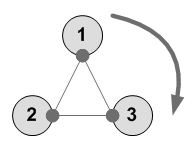
---------- 1 2 3 3 1 2 ----------
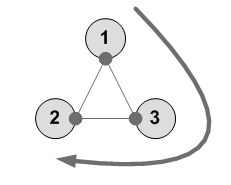
---------- 1 2 3 2 3 1 ----------
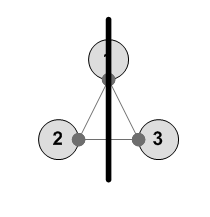
---------- 1 2 3 1 3 2 ----------
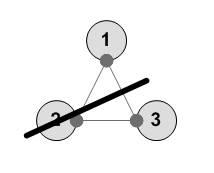
---------- 1 2 3 2 1 3 ----------
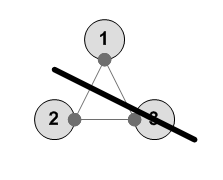
---------- 1 2 3 3 2 1 ----------
4
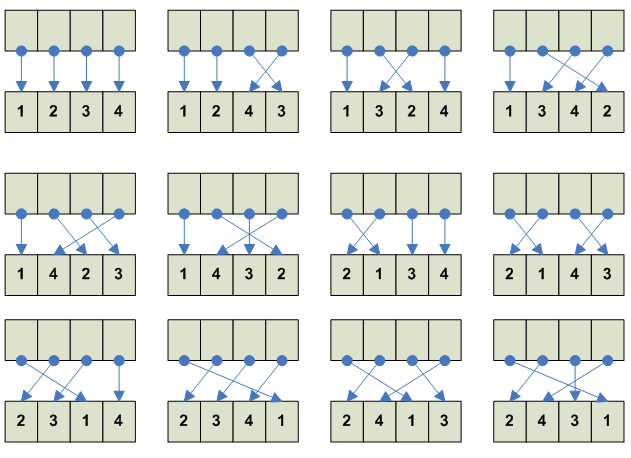
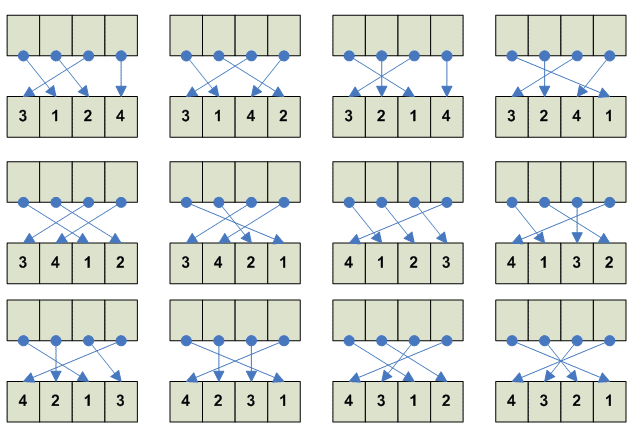
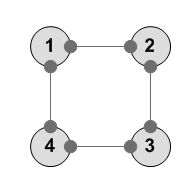
Тождество --------- 1 2 3 4 1 2 3 4 ---------
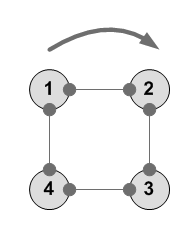
Вращение -90 --------- 1 2 3 4 4 1 2 3 ---------
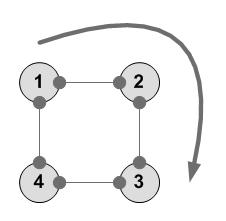
Вращение -180 --------- 1 2 3 4 3 4 1 2 ---------
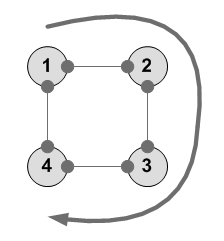
Вращение -270 --------- 1 2 3 4 2 3 4 1 ---------
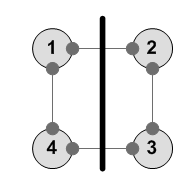
Отражение через вертикаль --------- 1 2 3 4 2 1 4 3 ---------
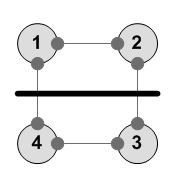
Отражение через горизонталь --------- 1 2 3 4 4 3 2 1 ---------
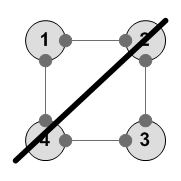
Отражение LD-RU диоганаль --------- 1 2 3 4 3 2 1 4 ---------
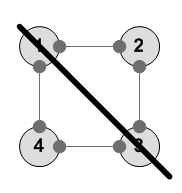
Отражение LU-RD диагональ --------- 1 2 3 4 1 4 3 2 ---------
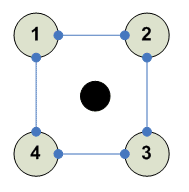
Отражение через центр --------- 1 2 3 4 3 4 1 2 --------- оно в данном случае экивалентно повороту на 180'
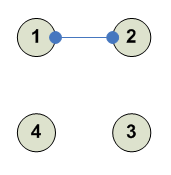
Вырожденный случай - обмен пары Таких случаев 6 - потому что 6 пар. --------- 1 2 3 4 (1 - 2) 2 1 3 4 --------- --------- 1 2 3 4 (1 - 3) 3 2 1 4 --------- --------- 1 2 3 4 (1 - 4) 4 2 3 1 --------- --------- 1 2 3 4 (2 - 3) 1 3 2 4 --------- --------- 1 2 3 4 (2 - 4) 1 4 3 2 --------- --------- 1 2 3 4 (3 - 4) 1 2 4 3 ---------
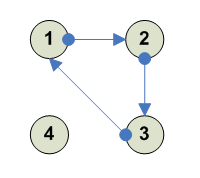
Вырожденный случай - вращение трешки вправо Таких случаев 4, потому что 4 трешки --------- 1 2 3 4 [123] 3 1 2 4 --------- --------- 1 2 3 4 [124] 4 1 3 2 --------- --------- 1 2 3 4 [134] 4 2 1 3 --------- --------- 1 2 3 4 [234] 1 4 2 3 ---------
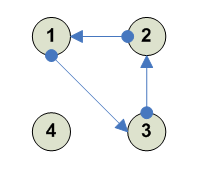
Вырожденный случай - вращение трешки влево Таких случаев 4, потому что 4 трешки --------- 1 2 3 4 [123] 2 3 1 4 --------- --------- 1 2 3 4 [124] 2 4 3 1 --------- --------- 1 2 3 4 [134] 3 2 4 1 --------- --------- 1 2 3 4 [234] 1 3 4 2 ---------
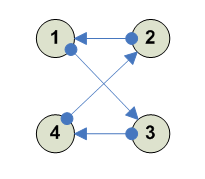
Вращение (только по другим переменным) ---------- 1 2 3 4 2 4 1 3 ----------
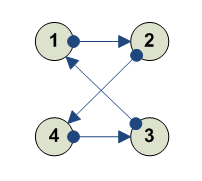
тоже но в обратную сторону ---------- 1 2 3 4 3 1 4 2 ----------
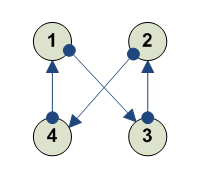
Еще одно вращение по другим переменным ---------- 1 2 3 4 4 3 1 2 ----------
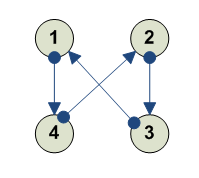
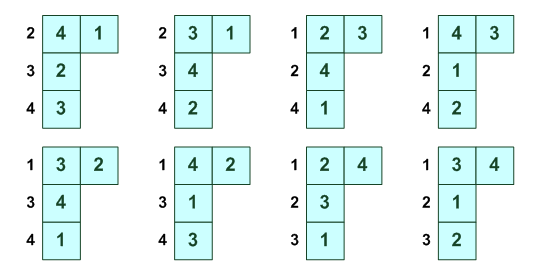
тоже но в обратную стророну ---------- 1 2 3 4 3 4 2 1 ---------- Всего перестановок 24 (мы их все описали базируясь на геометрическом смысле). Теперь полный список: ------------------------------------------- 1 2 3 4 e 1 2 4 3 обмен 3-4 1 3 2 4 обмен 2-3 1 3 4 2 вращение [234] влево 1 4 2 3 вращение [234] вправо 1 4 3 2 отражение по оси 1-3, обмен 2-4 2 1 3 4 обмен 1-2 2 1 4 3 отражение вертикаль 2 3 1 4 вращение [123] влево 2 3 4 1 поворот -270/+90 2 4 1 3 вращение вправо 2 4 3 1 вращение [124] влево 3 1 2 4 вращение [123] вправо 3 1 4 2 вращение 3 2 1 4 отражение по оси 2-4, обмен 1-3 3 2 4 1 вращение [134] влево 3 4 1 2 поворот -180/+180, отражение через центр 3 4 2 1 вращение 4 1 2 3 поворот -90/+270 4 1 3 2 вращение [124] вправо 4 2 1 3 вращение [134] вправо 4 2 3 1 обмен 1-4 4 3 1 2 вращение 4 3 2 1 отражение горизонталь -------------------------------------------
5
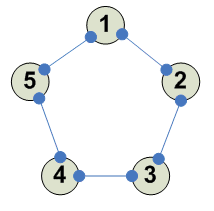
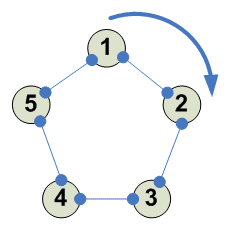
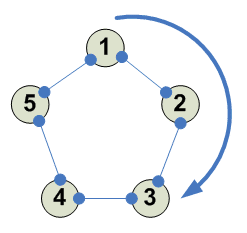
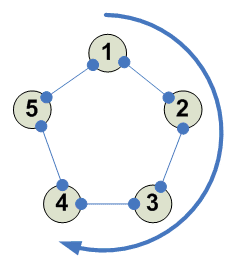
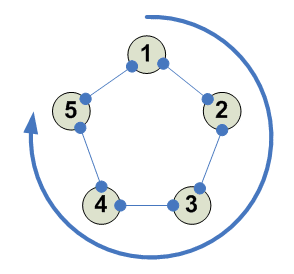
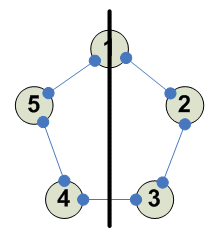
И 4 других аналогичных
6
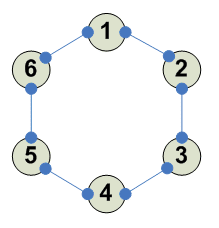
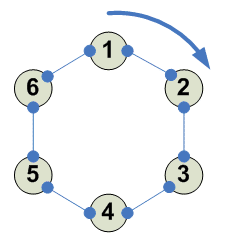
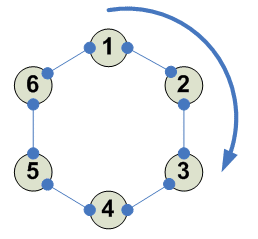
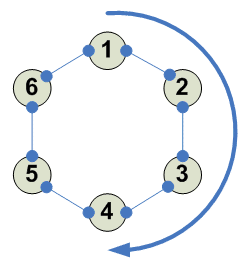
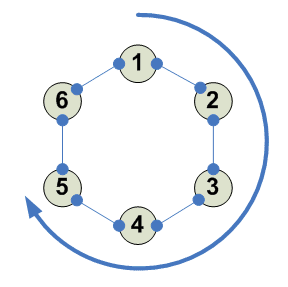
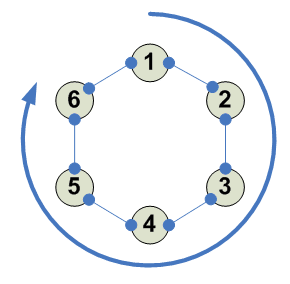
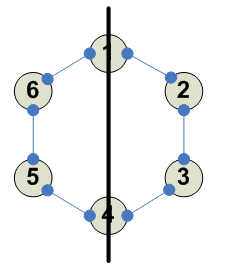
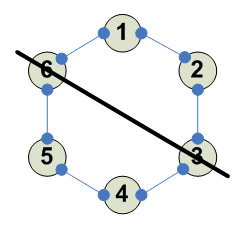
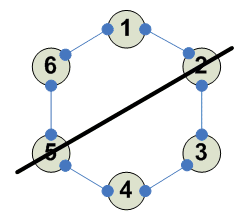
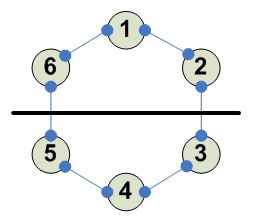
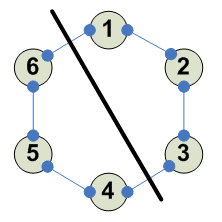
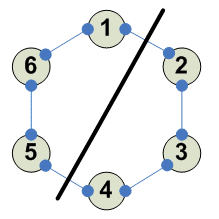
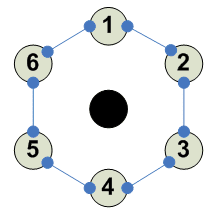
Разбиения

[1]
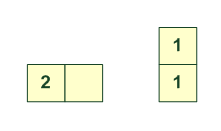
[2] [1,1]
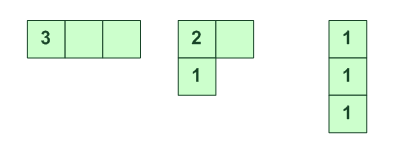
[3] [2,1] [1,1,1]
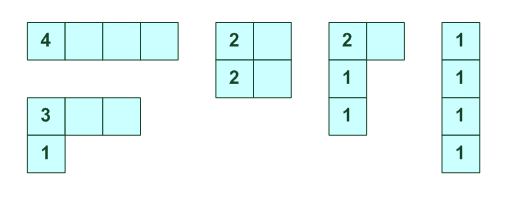
[4] [3,1] [2,2] [2,1,1] [1,1,1,1]
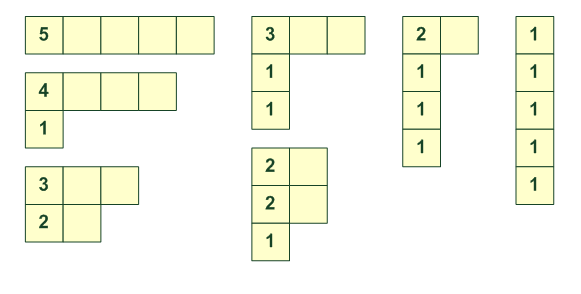
[5] [4,1] [3,2] [3,1,1] [2,2,1] [2,1,1,1] [1,1,1,1,1]
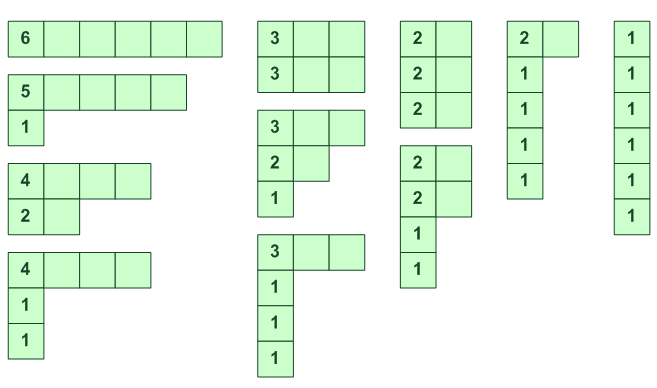
[6] [5,1] [4,2] [4,1,1] [3,3] [3,2,1] [3,1,1,1] [2,2,2] [2,2,1,1] [2,1,1,1,1] [1,1,1,1,1,1]
[7] [6,1] [5,2] [5,1,1] [4,3] [4,2,1] [4,1,1,1] [3,3,1] [3,2,2] [3,2,1,1] [3,1,1,1,1] [2,2,2,1] [2,2,1,1,1] [2,1,1,1,1,1] [1,1,1,1,1,1,1]
[8] [7,1] [6,2] [6,1,1] [5,3] [5,2,1] [5,1,1,1] [4,4] [4,3,1] [4,2,2] [4,2,1,1] [4,1,1,1,1] [3,3,2] [3,3,1,1] [3,2,2,1] [3,2,1,1,1] [3,1,1,1,1,1] [2,2,2,2] [2,2,2,1,1] [2,2,1,1,1,1] [2,1,1,1,1,1,1] [1,1,1,1,1,1,1,1]
Мультиномальные коэфициенты: Предположим что у нас 4 переменных, и 7 степень, нам подходят только те разбиения в которых число партиций не превышает 4. то есть число партиций [7] 1 - OK [6,1] 2 - OK [5,2] 2 - OK [5,1,1] 3 - OK [4,3] 2 - OK [4,2,1] 3 - OK [4,1,1,1] 4 - OK [3,3,1] 3 - OK [3,2,2] 3 - OK [3,2,1,1] 4 - OK [3,1,1,1,1] 5 - NONE [2,2,2,1] 4 - OK [2,2,1,1,1] 5 - NONE [2,1,1,1,1,1] 6 - NONE [1,1,1,1,1,1,1] 7 - NONE
Диаграммы Юнга и перестановки
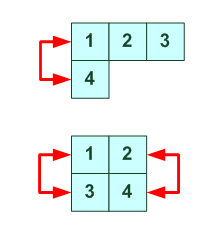
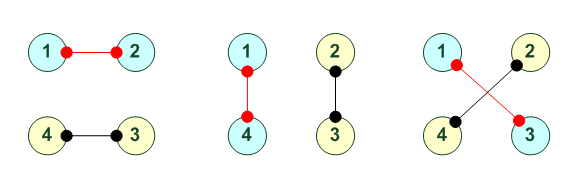
столбик из двух - это обмен
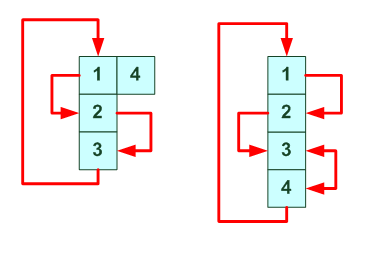
В принципе столбик это поворот (тройки или четверки). Ниже будут указаны результатирующие индексы для таких столбиков.

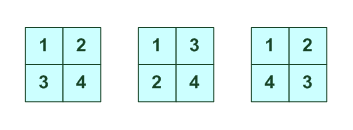
Тождество - оно одно 1234 ---------- 1 2 3 4 1 2 3 4 ----------
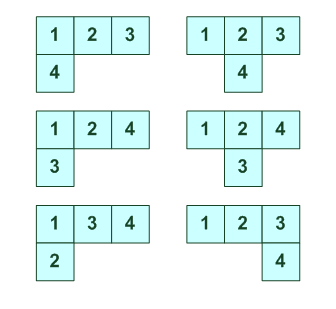
Обмен пары. Всего существует 6 вариантов: 123 123 4 4 ---------- ---------- 1 2 3 4 1 2 3 4 4 2 3 1 1 4 3 2 ---------- ---------- 124 124 3 3 ---------- ---------- 1 2 3 4 1 2 3 4 3 2 1 4 1 3 2 4 ---------- ---------- 134 123 2 4 ---------- ---------- 1 2 3 4 1 2 3 4 2 1 3 4 1 2 4 3 ---------- ----------
Обмен двух пар: 12 13 12 34 24 43 ---------- ---------- ---------- 1 2 3 4 1 2 3 4 1 2 3 4 3 4 1 2 2 1 4 3 4 3 2 1 ---------- ---------- ---------- Всего есть 3 варианта - двух пар.
Вращение троек: Всего есть 4 тройки, каждая может быть повернута вправо или влево. 41 31 23 43 2 4 4 1 3 2 1 2 ---------- ---------- ---------- ---------- 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 4 2 3 1 3 4 2 2 4 3 1 4 1 3 2 ---------- ---------- ---------- ---------- 32 42 24 34 4 1 3 1 1 3 1 2 ---------- ---------- ---------- ---------- 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 3 2 4 1 4 2 1 3 2 3 1 4 3 1 2 4 ---------- ---------- ---------- ----------
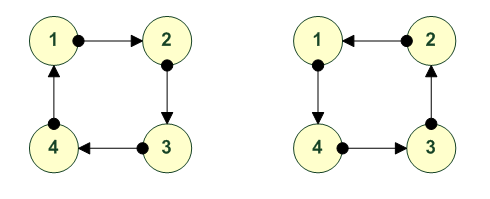
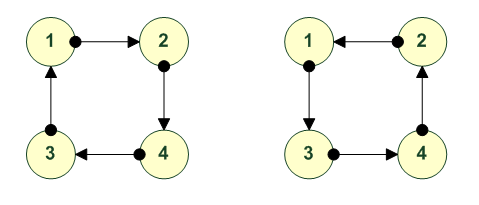
Вращения 2 4 3 1 4 2 1 3 ---------- ---------- 1 2 3 4 1 2 3 4 2 3 4 1 4 1 2 3 ---------- ---------- (1234)~> <~(1234)
2 3 3 4 4 1 4 3 1 4 2 1 3 2 1 2 ---------- ---------- ---------- ---------- 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 2 4 1 3 3 1 4 2 3 4 2 1 4 3 1 2 ---------- ---------- ---------- ---------- (1243)~> <~(1243) (1324)~> <~(1324)
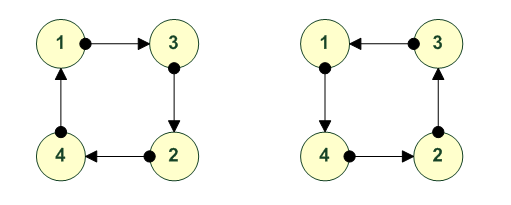
Почему вращений всего 6? 1 фиксируем на 1й позиции тогда возможные варианты: 1.234 1.243 1.324 1.342 = - 1.243 тоже но вращение в другую сторону 1.423 = - 1.324 тоже но вращение в другую сторону 1.432 = - 1.234 тоже но вращение в другую сторону 1234 left = 2341 = 3412 right 1234 right = 4123 = 3412 left 1243 left = 2431 = 4312 right 1243 right = 3124 = 4312 left 1324 left = 3241 = 2413 right 1324 right = 4132 = 2413 left
Композиции
2
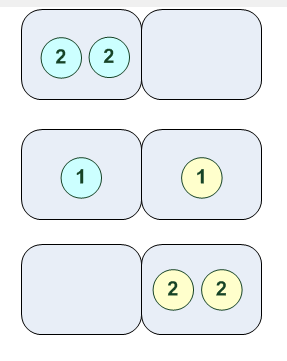
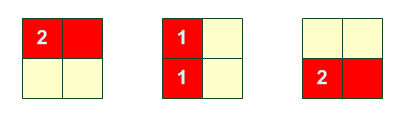
3
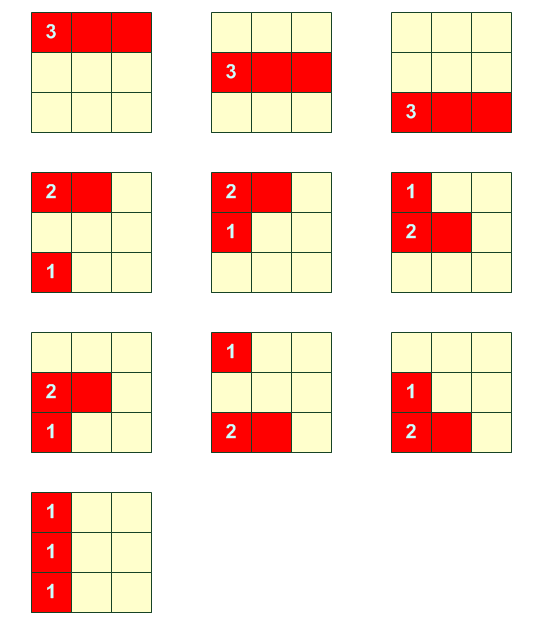
[3,0,0] [2,1,0] [2,0,1] [1,2,0] [1,1,1] [1,0,2] [0,3,0] [0,2,1] [0,1,2] [0,0,3]
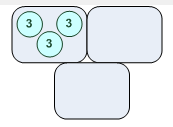
[3,0,0]
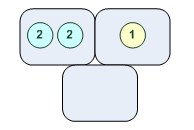
[2,1,0]
[2,0,1]
[1,2,0]
[1,1,1]
[1,0,2]
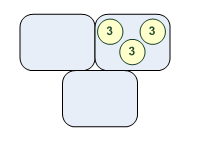
[0,3,0]
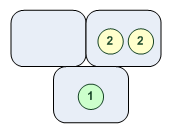
[0,2,1]
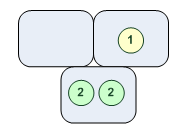
[0,1,2]
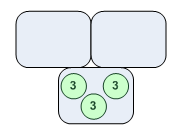
[0,0,3]