40.1. ЧИСЛА С ПЛАВАЮЩЕЙ ТОЧКОЙ

IEEE 754-1985 стандарт на числа с плавающей точкой (87,287,387 original не соответствуют стандарту) FP Number имеет формат: +-+-------+----------+ |S| E | M | +-+-------+----------+ S - Sign если = 0 то число положительное, если = 1 то число отрицательное E - Exponent - смещенная экспонента. .... 2**(-1) = N - 1 2** 0 = N , где N - смещение порядка 2** 1 = N + 1 (зависит от размера мантиссы) ... M - Mantiss - мантисса в обычном случае нормализованная (т.е. старший бит не записывается и равен 1. [точка справа старшего бита мантиссы] Число = (-1)^S * 2^(E-N) * 1.MMMMMMMMM, где MMMMMMM - биты мантиссы 1.MMMMMMMMMM <- неявная нормализация +-+-------+----------+ |S| E | M | +-+-------+----------+ Иногда при предельных значениях порядка неявная нормализация теряется и числа становятся денормализированными.

Single

Single занимает 32-бит (DWORD) К сожалению FP в памяти тоже подвержены endian. Single Big-Endian: ---------------------------------------- byte bits description ---------------------------------------- 0 0-6 exponent bits 1-7 7 sign 1 0-6 mantissa bits 16-22 7 exponent bit 0 2 0-7 mantissa bits 8-15 3 0-7 mantissa bits 0-7 ---------------------------------------- Single Little-endian: ---------------------------------------- byte bits description ---------------------------------------- 0 0-7 mantissa bits 0-7 1 0-7 mantissa bits 8-15 2 0-6 mantissa bits 16-22 7 exponent bit 0 3 0-6 exponent bit 1-7 7 sign ----------------------------------------

Double

Double занимает 64-бит (QWORD) Double big-endian: ---------------------------------------- byte bits description ---------------------------------------- 0 0-6 exponent 4-10 7 sign 1 0-3 mantissa 48-51 4-7 exponent 0-3 2 0-7 mantissa 40-47 3 0-7 mantissa 32-39 4 0-7 mantissa 24-31 5 0-7 mantissa 16-23 6 0-7 mantissa 8-15 7 0-7 mantissa 0-7 ---------------------------------------- Double little-endian: ---------------------------------------- byte bits description ---------------------------------------- 0 0-7 mantissa 0-7 1 0-7 mantissa 8-15 2 0-7 mantissa 16-23 3 0-7 mantissa 24-31 4 0-7 mantissa 32-39 5 0-7 mantissa 40-47 6 0-3 mantissa 48-51 4-7 exponent 0-3 7 0-6 exponent 4-10 7 sign ----------------------------------------

Quad

Quad занимает 128-бит (OWORD) Соответсвенно endian.

Extended (Intel)

Extended - платформо-зависимый, занимает на Intel 80-бит (TBYTE) Поскольку Intel то Little-endian.

Параметры FP

------------------------------------------------------------- Single Double Extended Quad ------------------------------------------------------------- Len bits 32 64 80 128 M bits 24* 53* 64 113* E bits 8 11 15 15 E max +127 +1023 +16383 +16383 E min -126 -1022 -16382 -16382 N 127 1023 16383 16383 ------------------------------------------------------------- 1.188 * 10^-38 < | Single | < 3.40 * 10^38 2.23 * 10^-308 < | Double | < 1.79 * 10^308 3.37 * 10^-4932 < | Quad | < 1.18 * 10^4932 log{2}(10) ~= 3.3 двоичных разряда на десятичную цифру Мантисса длинной 20 (для примера) бит держит 20/3.3 = 6.06 десятичных цифр

Специальные числа

0 имеет все биты равными нулю. Бесконечность:

NaN:

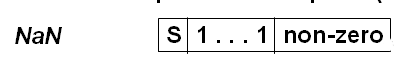
Денормализованные числа

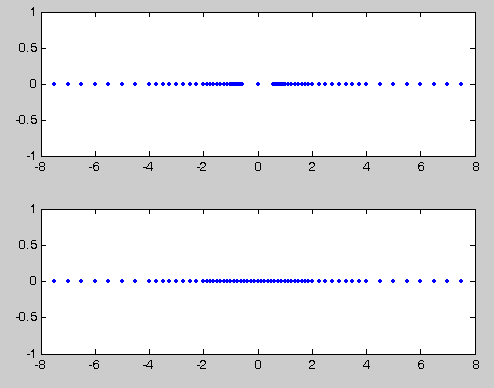
Если использовать только нормализовааные числа, то вокруг нуля естественным образом возникает "мертвая зона", размер которой существенно превышает расстояния между соседними числами вне мертвой зоны. Пример для числел вида seemmm: (Верхний график - денормализация для чисел близких к нулю не используется, нижний график - денормализация для чисел близких к нулю используется)

Поэтому вблизи нуля используется денормализованные числа. +-+-------+---------------+ |S|00.. 00|000.........000| 0 +-+-------+---------------+ +-+-------+---------------+ |S|00.. 00| M | Denormalized number +-+-------+---------------+

Обычные числа трактуются как: (-1)^S * 2^(E-N) * 1.MMMMMMMM +-+--------+-----------------------+ |0|00000001|00000000000000000000000| +-+--------+-----------------------+ (-1)^0 * 2^(1-127) * 1.MMM = 2^(-126) * 1.0000000000.. Денормализованные числа трактуются как: (-1)^S * 2^(E-N+1) * 0.MMMMMMMM Экспонента на самом деле равна не 0, а 1 +-+--------+-----------------------+ |0|00000000|11111111111111111111111| +-+--------+-----------------------+ (-1)^0 * 2^(0-127+1) * 0.MMMM = 2^(-126) * 0.111111111..

Примеры FP

Single -infinity FF80 0000 -2 C000 0000 -1 BF80 0000 -0.5 BF00 0000 -0.0 8000 0000 +0.0 0000 0000 0000 0001 minimal demormalized positive 007F FFFF maximal denormalized positive 0.5 3F00 0000 1 3F80 0000 2 4000 0000 3 4040 0000 4 4080 0000 5 40A0 0000 6 40C0 0000 7 40E0 0000 8 4100 0000 9 4110 0000 10 4120 0000 15 4170 0000 16 4180 0000 2^24 4B80 0000 2^31 4F00 0000 2^32 4F80 0000 2^64 5F80 0000 7F7F FFFF maximal normalized +infinity 7F80 0000 7F80 0001 minimal SNaN 7FBF FFFF maximal SNaN 7FC0 0000 minimal QNaN 7FFF FFFF maximal QNaN Double -infinity FFF0 0000 0000 0000 -2 C000 0000 0000 0000 -1 BFF0 0000 0000 0000 -0.5 BFE0 0000 0000 0000 -0.0 8000 0000 0000 0000 +0.0 0000 0000 0000 0000 0000 0000 0000 0001 minimal denormalized positive 000F FFFF FFFF FFFF maximal denormalized positive 0.5 3FE0 0000 0000 0000 1 3FF0 0000 0000 0000 2 4000 0000 0000 0000 3 4008 0000 0000 0000 4 4010 0000 0000 0000 5 4014 0000 0000 0000 6 4018 0000 0000 0000 7 401C 0000 0000 0000 8 4020 0000 0000 0000 9 4022 0000 0000 0000 10 4024 0000 0000 0000 15 402E 0000 0000 0000 16 4030 0000 0000 0000 2^24 4170 0000 0000 0000 2^31 41E0 0000 0000 0000 2^32 41F0 0000 0000 0000 2^64 43F0 0000 0000 0000 7FEF FFFF FFFF FFFF maximal normalized +infinity 7FF0 0000 0000 0000 7FF0 0000 0000 0001 minimal SNaN 7FF7 FFFF FFFF FFFF maximal SNaN 7FF8 0000 0000 0000 minimal QNaN 7FFF FFFF FFFF FFFF maximal QNaN

попробуем перевести 1.0: S = 0 E = 0 M = 1.000000 S EEEE EEEE MMM...MMMM 0 0000 0000 1.000...0000 + 0111 1111 = N ---------------------------------- 0 0111 1111 000...0000 +---++---++---------------+...+--+ 3 F 8 00s 0 3F80 0000

NaN

NaN - Not a Number - не число - не представимое число которое может возникать во всяких специальных случаях типа: 0 / 0 корень квадратный (-1) NaN / \ SNaN QNaN SNaN - signaled NaN - модуль FP никогда не создает такие числа (используются для exceptions) QNaN - not signaled NaN - модуль FP может их создавать NaN не стандартизированны: PowerPC,x86: high bit of M = 0 SNaN = 1 QNaN Alpha,HPPA,MIPS: high bit of M = 0 QNaN = 1 SNaN

Правила вычислений

x - нормальное представимое число (не 0, не infinity, не NaN) x + +infinity = +infinity x - +infinity = -infinity x + -infinity = -infinity x - -infinity = +infinity x * +infinity = +infinity x / +infinity = 0 (знак зависит от x) +infinity + +infinity = +infinity -infinity + -infinity = -infinity -infinity - +infinity = -infinity +infinity - -infinity = +infinity +infinity + -infinity = NaN -infinity + +infinity = NaN +infinity - +infinity = NaN -infinity - -infinity = NaN 0 * infinity = NaN 0 / 0 = NaN infinity / infinity = NaN x MOD 0 = NaN infinity MOD x = NaN квадратный корень(x) = NaN (если x < 0) Любая операция с SNaN всегда дает NaN

Числовая прямая

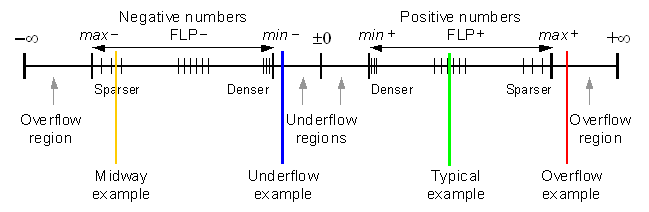
Используется аффинный (Affine) режим:

-infinity -0 +0 +infinity | -x | +x | |-----------------------|------------------------| -infinity -0 +0 -infinity | | | |---------|------|---|---|---|---|--------|-------| O N D U U D N O O = Overlow Zone N = Normalized Zone D = Denormalized Zone U = Underflow Zone Eще есть проективный режим но он не входит в IEEE 754 (ранние [до принятия стандарта IEEE754] сопроцессоры 87, 287 могли его использовать)

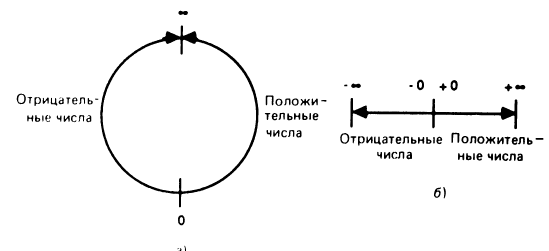
Аффинный Проективный +0.0 0.0 -0.0 +infinity infinity -infinity

Режимы округления

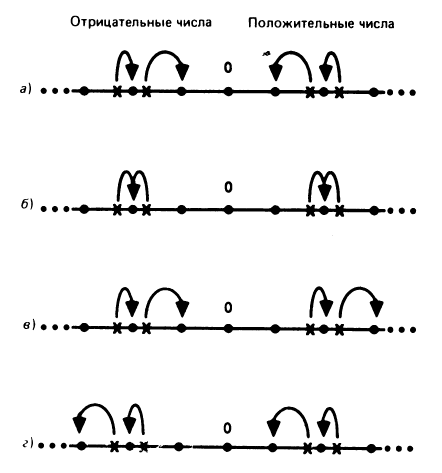
Округление к 0 Округление к ближайшему Округление к +бесконечности Округление к -бесконечности

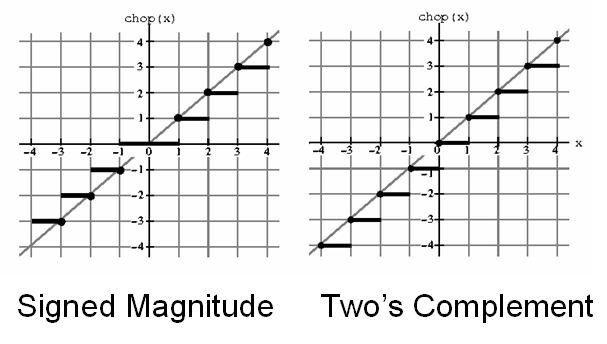
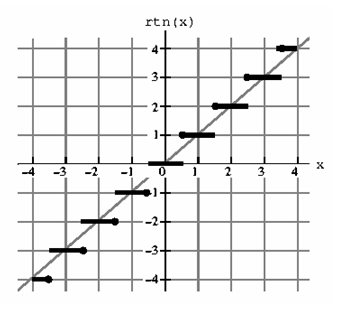
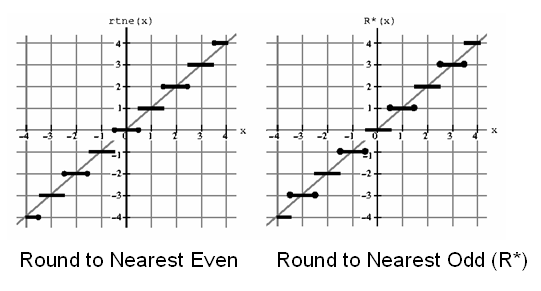
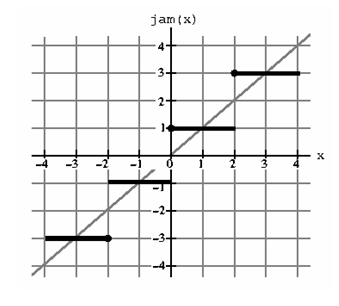
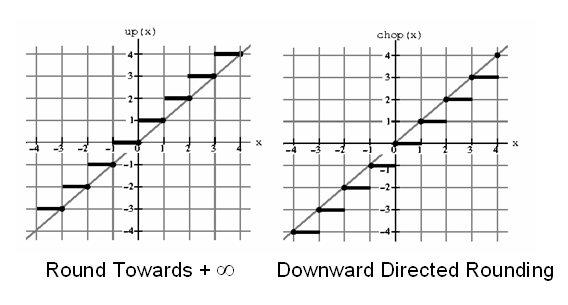
Другие FP форматы:

Cray: Формат чисел с плавающей точкой на CRAY-1 ----------------------- Bits Description ----------------------- 0 Sign 1..15 Exponent 16..63 Mantiss -----------------------

VAX: --------------------------------------------------------------- Number BITS Type exponent fraction total N --------------------------------------------------------------- F float 8 23 32 128 D float 8 55 64 128 G float 11 52 64 1024 H float 15 112 128 16384 --------------------------------------------------------------- тоже нормализованные (в отличии от IEEE 754 точка слева от скрытой единицы). не поддерживает NaN и бесконечность. Для всех VAX форматов мантисса нормализуется так чтобы 0.5 <= f < 1.0 MSB мантиссы - всегда 1 и не записывается.

F-Float:

---------------------------------------- byte bits description ---------------------------------------- 0 0-6 mantissa bits 16-22 7 exponent bit 0 1 0-6 exponent bit 1-7 7 sign bit 2 0-7 mantissa bits 0-7 3 0-7 mantissa bits 8-15 ---------------------------------------- 0 00000000 (really Sign=0, Exponent=0, mantiss=don't care (VAX) but for Alpha if mantiss != 0 it caused exception) +1.0 00004080 (mantiss = (.1)0, exponent = 129) +1.5 000040C0 (mantiss = (.1)1, exponent = 129)

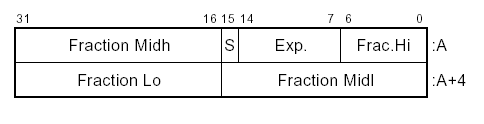
D-float: ---------------------------------------- byte bits description ---------------------------------------- 0 0-6 mantissa 48-54 7 exponent 0 1 0-6 exponent 1-7 7 sign 2 0-7 mantissa 32-39 3 0-7 mantissa 40-47 4 0-7 mantissa 16-23 5 0-7 mantissa 24-31 6 0-7 mantissa 0-7 7 0-7 mantissa 8-16 ----------------------------------------

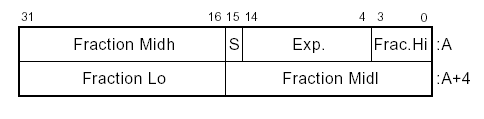
G-float: ---------------------------------------- byte bits description ---------------------------------------- 0 0-3 mantissa 48-51 4-7 exponent 0-3 1 0-6 exponent 4-10 7 sign 2 0-7 mantissa 32-39 3 0-7 mantissa 40-47 4 0-7 mantissa 16-23 5 0-7 mantissa 24-31 6 0-7 mantissa 0-7 7 0-7 mantissa 8-15 ---------------------------------------- Что значит точка слева от скрытой единицы: IEEE754 S E M 1.0 = 1 * 2^0 0 01111111 (1.)00000000000000000000000 0 1.0 = 3F000000 MSB LSB VAX F float 1.0 = 0.1 * 2^1 0 10000001 (.1)00000000000000000000000 1 1.0 = 40800000 но учитывая расположение в памяти получаем: 00004080 MSB LSB

Во время 8-битных машин когда в микропроцессорах не был встроен блок операций с плавающей точкой из MS-BASIC использовался тип для программных операций с плавающей точкой (MSFLOAT). MSFLOAT = REAL48 MSB +-+----------------+-----+ |S| M | E | +-+----------------+-----+ 1 39 8 В отличие от IEEE 754 имеет поменянные местами мантиссу и экспоненту. Real48 тоже храниться нормализованным: N = if E == 0, then 0 if E != 0, then (-1)^S * 2^(E-129) * (1.M) 2.9 * 10^-39 < | Real | < 1.7*10^38

Index Prev Next