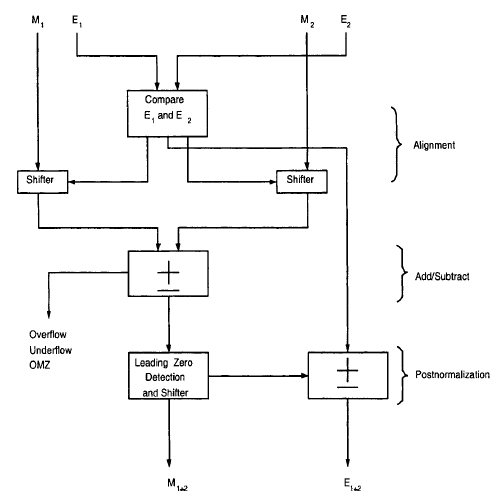
сложение/вычитание


C = A + B WE = MAX(A.E, B.E) // берем максимальную экспоненту WAM = DENORMALIZE(A,WE) // денормализуем по нужной экспоненте WBM = DENORMALIZE(B,WE) NM = WAM + WBM // проверим CF if CF = 1 { NE = WE + 1 } else { NE = WE } C.E = NE C.M = NM C.S = знак того кто больше
умножение




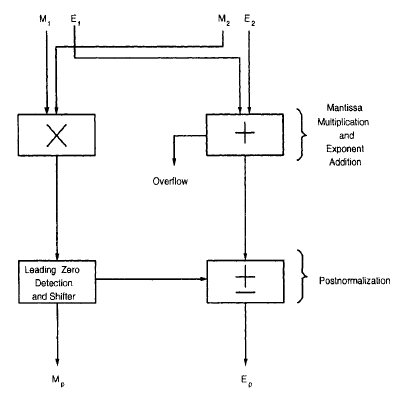
C = A * B C.E = A.E + B.E C.S = A.S + B.S // по модулю 2 C.M = DENORMALIZE(A.M) * DENORMALIZE(B.M)
деление




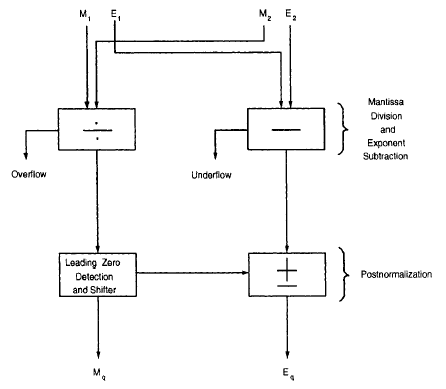
C = A / B C.E = A.E - B.E C.S = A.S + B.S // по модулю 2 C.M = DENORMALIZE(A.M) / DENORMALIZE(B.M)
Квадратный корень

Пусть есть число = S * p^k тогда, если k - четное, то SQRT(S * p^k) = SQRT(S) * p^(k/2) а если нечетное, то SQRT(S * p^k) = SQRT(S * p * p^(k-1)) = SQRT(S*p) * p^((k-1)/2)
Основы вычисления квадратного корня:

Идея: SQRT[Z] = SQRT[(A+B)^2] = SQRT[A^2 + 2AB + B^2] Рассмотрим простой случай - корень из 3-4 значного числа: ______ / 2 \/(a+b) ____________ / 2 2 _______ \/ a + 2ab + b возьмем например \/ 150 ____________ / 2 2 1.50 \/ a + 2ab + b = a 1.00 a = 1 * 10 = 10 2 -a ____________ / 2 2 1.50 \/ a + 2ab + b = a 1.00 2 ---- -a 50 = 2ab + b^2 --- 2 2ab + b 2 разделим теперь 2ab+b на 2а: 2 2ab + b 2ab -------- ~= --- ~= b потому что a >> b 2a 2a таким образом мы узнаем b: 50 / 2a = 50 / 20 = 2... значет следущая цифра это 2. ____________ / 2 2 \/ a + 2ab + b = a + b 2 -a --- 2 2ab + b - (2a + b) * b ------------- 0 проверим: 12^2 = 144 < 150 < 169 = 13^2
Рассмотрим более сложный случай (корень из 5-6 значного числа): _______ / 2 \/(a+b+c) (a+b+c)*(a+b+c) = a^2 + ab + ac + ab + b^2 + bc + ac + bc + c^2 = = a^2 + 2ab + b^2 + 2ac + 2bc + c^2 = = a^2 + 2ab + b^2 + 2(a+b)*c + c^2 ___________________________ / 2 2 2 \/ a + 2ab + b + 2(a+b)*c + c по аналогии с случаем 3-4 значного числа: ___________________________ / 2 2 2 \/ a + 2ab + b + 2(a+b)*c + c 2 -a --- 2 2ab + b - (2a + b) * b ------------------------------ 2 2(a+b)*c + c -(2(a+b) + c) *c ---------------- 0 Проиллюстрируем: __________ \/ 28.72.96 25 первая цифра пять - типа полный квадрат который влез --- 3.72 372 = 2*5*b + b^2 . 372/2a = 372/(2*5*10) = 372/100 = 3,.. (дробная часть неважна) . (10 - потому что 5 на 1 порядок старше) 3.09 (2a+b)*b = (2*5*10 + 3)*3 = 103 * 3 = 109 -------- 63.96 6696 = 2*(a+b)*c + c^2 . 6696/[2(a+b)] = 6696/(2*(5*100 + 3*10) = (5 на 2 порядка, 3 на порядок) . = 6696/(2*530) = 6696/1060 = 6,... (дробная часть неважна) . (2(a+b)+c) * c = (2*(500+30) + 6)*6 = 1066 * 6 = 6396 63.96 ----- 0 таким образом: ________ \/ 287296 = 536
Специальные случаи которые могут возникать в десятичной системе. ____________ \/ 3'25,80'25 1 --- (случай 1) 225 225 = 2ab + b^2 . 225 / 2a = 225 / (2*1*10) = 225 / 20 = 11 (!) . 11 это уже больше чем цифра поэтому берем мах цифру = 9 . . (случай 2) . (2ab + b^2) = (2*1*10 + 9) * 9 = 29 * 9 = 261 > 225 (!) . значит 9 - это слишком большая цифра - поэтому берем 8 224, (2ab + b^2) = (2*1*10 + 8) * 8 = 28 * 8 = 224 < 225 Ok ------ 180 180 = 2*(a+b)*c + c^2 . 180 / 2(a+b) = 180 / 2*(1*100 + 8*10) = 180/2*(180) = 180/360=0,.. 000 цифра будет 0 итд (кстати если будем пересекать десятичную точку то продолжаем считать частичный корень как целое число).
_________ \/0,00'00'28 . (случай 3) . лидирующие пары нули можно сразу писать в результат . как 0 за каждую пару 0,00'00 Начало результата = 0,0 ---------- 28 25 5 ---- 300 300/100 = 3, но 103*3 = 309 > 300, поэтому 2 204 поэтому 2 ---- 9600 9 9441 ----- итд результат примерно равен 0,00529
Аналогично для 7-8 значного и более старших чисел: _________ ___________________________________________ / 2 / 2 2 2 2 \/(a+b+c+d) = \/ a + 2ab + b + 2(a+b)*c + c + 2(a+b+c)d + d ___________ _____________________________________________________________ / 2 / 2 2 2 2 2 \/(a+b+c+d+e) = \/ a + 2ab + b + 2(a+b)*c + c + 2(a+b+c)d + d + 2(a+b+c+d)e + e
Вычисление квадратного корня в двоичной системе: (оно самое простое так как нет сложных случаев) ____________ / 2 2 \/ a + 2ab + b = a 2 -a --- 2 2ab + b Заметим что в двоичной системе у нас только 2 цифры 0 и 1 соответсвенно 2 2аb + b может быть равно либо 0 если b = 0 2a + 1 если b = 1 2 2(a+b)c + c может быть равно либо 0 если с = 0 2(a+b) + 1 если с = 1 итд заметим что: 2a + 1 = (a << 1) + 1 то есть если, a или a+b итд - число вида xxxx то 2 2ab + b будет иметь вид xxxx01 если b = 1 (сдвиг на 1 бит потому что a на порядок больше и еще на один потому что умножается на 2)
Пример: ___________ \/ 1100010 {2} надо вычислить 01.10.00.10, делим на группы по 2 цифры ----------------------------------------- Сравнение Цифра Частичный корень ----------------------------------------- 01.10.00.10, 0 -- 01. >= 01 да 1 1 01. ----- 0.10 >= 1.01 нет 0 10 ----- 10.00 >= 10.01 нет 0 100 -------- 10.00.10 >= 100.01 да 1 1001 1.00.01, ---------- обратим внимание дошли до запятой - можем продолжать и дальше 1.00.01,00 >= 1001.01 да 1 1001,1 10.01,01 ------------------ 1.11,11.00 >= 10011.01 да 1 1001,11 1.00,11.01 --------------- 10,11.11.00 >= 100111.01 да 1 1001,111 10,01.11.01 итд Проверим: 1001 * 1001 ------------ 1001 0000 0000 1001 ------------ 1010001 1010 * 1010 ------------ 0000 1010 0000 1010 ----------- 1100100 1100100 больше 1100010 1010001 меньше так что квадратный корень мы нашли правильно Соответсвенно квадратный корень в двоичной системе относительно легко вычисляется (не на много сложнее деления).