2i
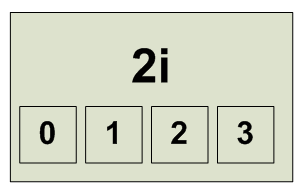
МНИМОЧЕТВЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ Основание системы счисления: 2i Цифры {0,1,2,3} Базис для системы с основанием 2i на комплексной плоскости:

--------------------- P (2I)^P --------------------- 8 256 7 -128I 6 -64 5 32I 4 16 3 -8I 2 -4 1 2I 0 1 -1 -I/2 -2 -1/4 -3 I/8 -4 1/16 -5 -I/32 -6 -1/64 -7 I/128 -8 1/256 --------------------- Интересное свойство: любое комплексное число может быть представленно в мнимочетверичной системе (без применения знака минус). 0 = 0 1 = 1 2 = 2 3 = 3 10 = 2i 11 = 2i + 1 12 = 2i + 2 13 = 2i + 3 20 = 4i 21 = 4i + 1 22 = 4i + 2 23 = 4i + 3 30 = 6i 31 = 6i + 1 32 = 6i + 2 33 = 6i + 3 100 = -4 101 = -3 102 = -2 103 = -1 110 = -4 + 2i 111 = -3 + 2i 112 = -2 + 2i 113 = -1 + 2i 120 = -4 + 4i 121 = -3 + 4i 122 = -2 + 4i 123 = -1 + 4i 130 = -4 + 6i 131 = -3 + 6i 132 = -2 + 6i 133 = -1 + 6i 210 = -8 + 2i 211 = -7 + 2i 212 = -6 + 2i 213 = -5 + 2i 1000 = -8i 10000 = 16 Некоторые нечетные мнимые числа выражаются дробями: 10.2 = i 1 * (2i) + 0*1 + 2 * (1 / 2i) = 2i + 2 / 2i = 2i - i = i | | +------+ | V --------------------------------------------------------------------------------- a1 b1 a2 b2 a1 a2 b1 b2 a2^2 b2^2 2/2i = (2, 0) / (0, 2) = ( (2*0 + 0 * 2) / (0 + 4 ) , (0*0 - 2*2) / (0 + 4)) = = ( 0, -1) = -i --------------------------------------------------------------------------------- (a{2n}...a[1] a[0] a[-1]...A[-2k]) {2i} = (a[2n]...a[2]a[0]a[-2]...a[-2k]) {-4} + 2i *(a[2n-1]...a[3] a[1] a[-1].... a[-2k+1]) {-4} Дробные числа: ------------------------------- .00 0 .01 -1/4 .02 -1/2 .03 -3/4 .10 -I/2 .11 -1/4 - I/2 .12 -1/2 - I/2 .13 -3/4 - I/2 .20 -I .21 -1/4 - I .22 -1/2 - I .23 -3/4 - I .30 -3I/2 .31 -1/4 - 3I/2 .32 -1/2 - 3I/2 .33 -3/4 - 3I/2 .00103 I/32 = I/8 + 3*(-I/32) .00102 I/16 = I/8 + 2*(-I/32) .001 I/8 .002 I/4 10.3 I/2 = 2I + 3*(-I/2) 10.2 I = 2I + 2*(-I/2) .1 -I/2 .102 -I/4 = -I/2 + 2*(I/8) .103 -I/8 = -I/2 + 3*(I/8) .0001 1/16 .0002 1/8 1.03 1/4 = 1 - 3/4 1.02 1/2 = 1 - 1/2 1. 1 .02 -1/2 .01 -1/4 .0102 -1/8 = -1/4 + 2*(1/16) .0103 -1/16 = -1/4 + 3*(1/16) -------------------------------
-i+1
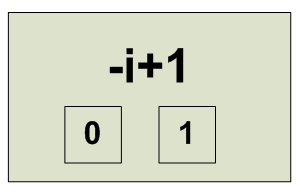
Система счистления с основанием (-i+1), где i - квадратный корень (-1) позволяет выразить любое целое комплексное число Цифры: 1 и 0 { 0, 1 } a + b*i = (qr + qi * i) (-1 + i) + r r = 0 or 1 qr = (b - a + r)/2 qi = (-a -b + r)/2 Если a и b оба четные/нечетные то r = 0 Если четность a и b разные то r = 1 (aN...a1a0){-1+i} = aN * (-1_i)^N + ... + a2 * (-1+i)^2 + + a1 * (-1+i) + a0 Базис для системы с основанием -i+1 на комплексной плоскости:
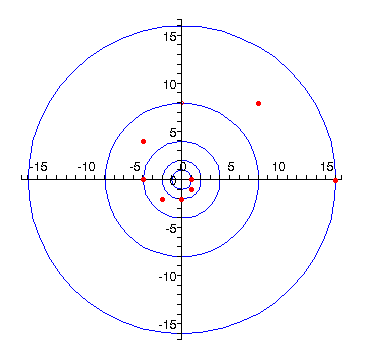
--------------------- P (-I+1)^P --------------------- 8 16 7 8 + 8I 6 8I 5 -4 + 4I 4 -4 3 -2 - 2I 2 -2I 1 1 - I 0 1 -1 (1 + I)/2 -2 I/2 -3 (-1 + I)/4 -4 -1/4 -5 (-1 - I)/8 -6 -I/8 -7 (1 - I)/16 -8 1/16 ---------------------
Числа: 0000 0 0001 1 0010 -1+i 0011 i 0100 -2i 0101 1-2i 0111 -i 1000 2+2i 1001 3+2i 1010 1+3i 1011 2+3i 1100 2 1101 3 1110 1+i 1111 2+i
Правила сложения: 1 + 1 = 1100 1 + 1 + 1 = 1101 1 + 1 + 1 + 1 = 111010000 1 + 1 + 1 + 1 + 1 = 111010001 1 + 1 + 1 + 1 + 1 + 1 = 111011100 1 + 1 + 1 + 1 + 1 + 1 + 1 = 111011101 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 111000000
-1+i
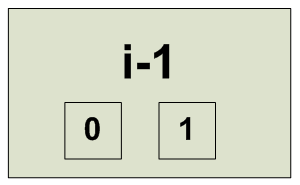
-1+i = -(-i+1) Сопряженные системы. Битовая строка представляющая число a+bi в одной из этих систем представляет a-bi. Пример {-i+1} {-1+i} 10
-2i
СИСТЕМА СЧИСЛЕНИЯ С ОСНОВАНИЕМ -2i Однозначно отображается в систему с основанием -1+i, которая является сопряжнной системе с основанием -i+1 которую мы рассмотрели. --------------------- {-2i} {-1+i} {10} --------------------- 0 00 0 1 01 1 2 10 -1+i 3 11 i ---------------------