71.4.1. СПЕКТР И ПРЕОБРАЗОВАНИЕ ФУРЬЕ

 
  THIS SECTION IS UNDER CONSTRUCTION  
 




  
  Спектр 
 

Любой переодический сигнал можно представить в виде ряда Фурье
(разложение Фурье).

Пример сложения двух синусоид:
(это диаграмма - амплитуда (Y)/время (X))
  


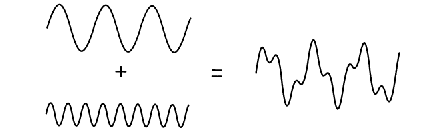
Спектр сложения двух синусоид:
(это диаграмма - амплитуда (Y)/частота(X))
  


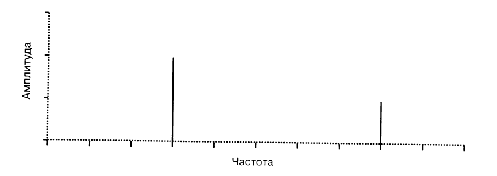
Можно сравнить что короче (длинный массив выборок амплитуда-время
или пара чисел частот).

Вот так выглядит спектр реального звука:
  




  
  Основы  
 


Как узнать входит ли частота или нет?
Умножить на синусоиду с частотой и сложить.
Если входит то сигнал будет отличаться от нуля
  

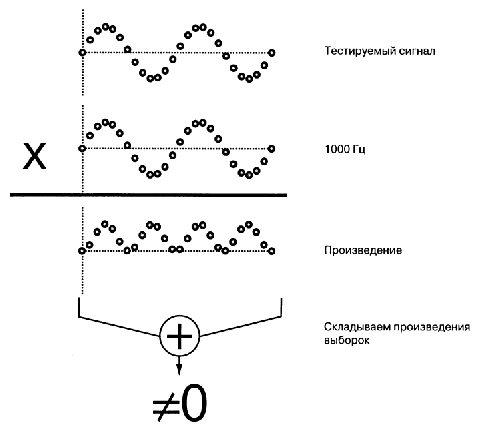
Если не входит то будет близок к нулю
  


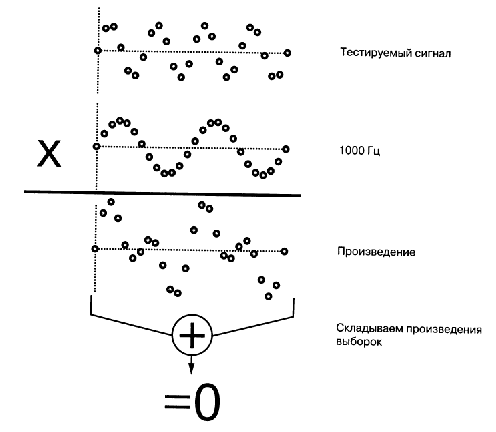
Как правило для обработки берут кусок от 32-1024 отчетов.




  
  Преобразование фурье 
 

Преобразование Фурье:
  


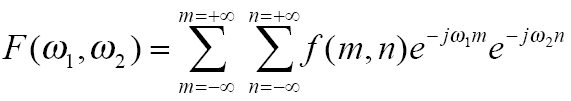
Обратное преобразование Фурье:
  



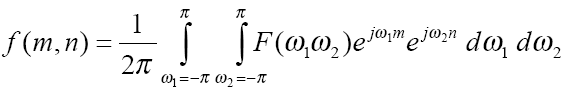
Дискретное преобразование Фурье:
  


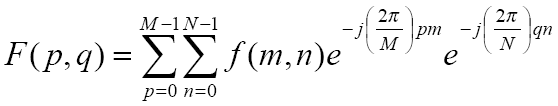
Обратное дискретное преобразование Фурье:
  


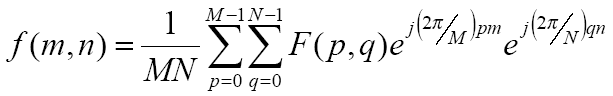
В пространстве Фурье image имеет два типа информации:
	Реальная часть:
		Амплитуда волны
		Информация о частотах волн
	Мнимая часть:
		Фаза волны
		Структура image


Пример первых функций для двухмерного ДПФ:
  





  
  Дискретное косинусное преобразование 
 


Дискретное косинусное преобразование (ДКП):
  


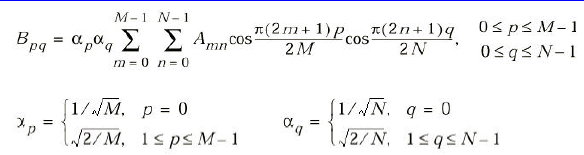
Обратное ДКП:
  


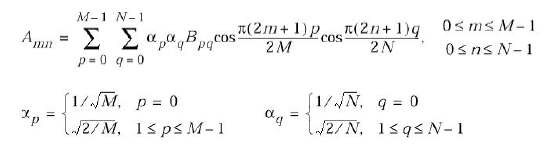
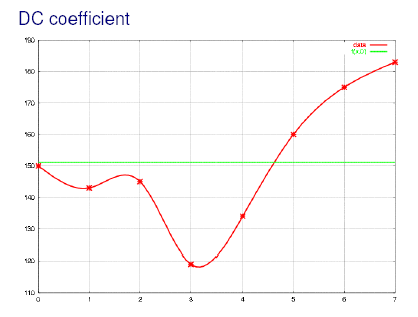
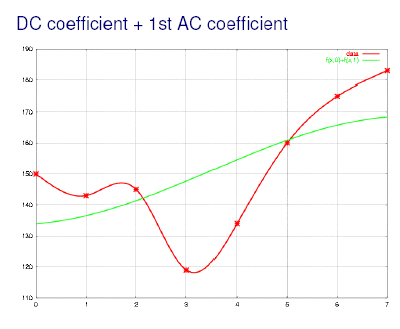
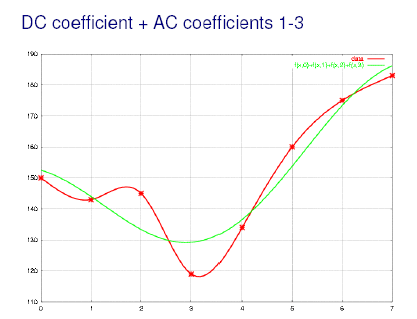
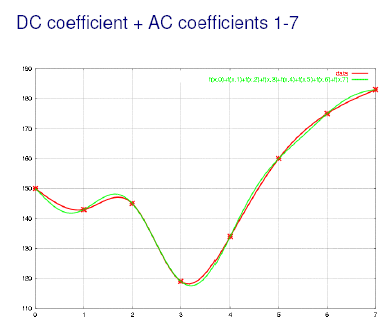
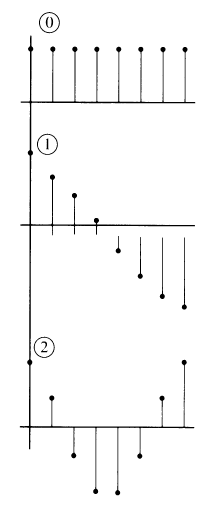
Пример первых частот ДКП для 1D случая (звук):
  

  

  


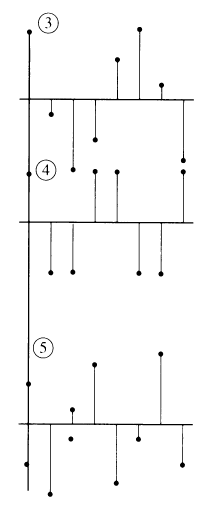
Пример первых частот ДКП для 2D случая (картинка):
  


Пример результатов ДКП: