3.13. КОМПЛЕКСНЫЕ ЧИСЛА

  


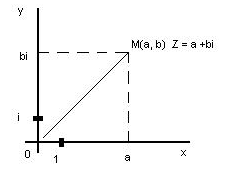
Обобщение линии действительных чисел на плоскость.
Идея - перпендикулярное к действительной оси направление определяется
корнем из -1 (не имеет рашений в действительных числах)

  




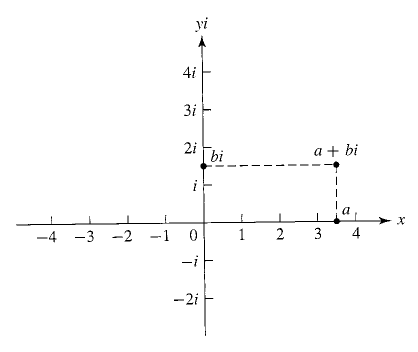
Запись	{a,b} - означает   а + b*i, где i - квадратный корень из (-1)
так называемая мнимая единица

i - корень уравнения	X^2 + 1 = 0

	т.к. (a + b) * (a - b) = a^2 + ab - ab - b^2 = a^2 - b^2
	то мы можем разложить X^2 + 1

	X^2 + 1 = (X + i)*(X - i) = 0

	корни  i и -i

Действительные числа - частный случай комплексных.




  
  Сложение и вычитание 
 

  



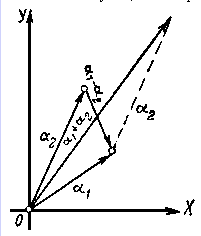
{a1, b1} + {a2, b2}  = {a1 + a2, b1 + b2}
{a1, b1} - {a2, b2}  = {a1 - a2, b1 - b2}




  
  Умножение 
 

  


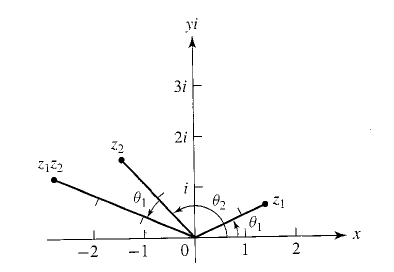
{a1, b1} * {a2, b2}  = {a1*a2 - b1*b2, b1*a2 + a1*b2}



  
  Деление 
 

{a1, b1} / {a2, b2} = { (a1*a2+b1*b2)/(a2^2+b2^2), (b1*a2-a1*b2)/(a2^2+b2^2) }

 a + b*i     a + b*i     c - d*i     a*c + b*d      b*c - a*d
--------- = --------- * --------- =  ----------  + ----------- i 
 c + d*i     c + d*i     c - d*i     c^2 + d^2     c^2 + d^2





  
  Тригонометрическая форма 
 

  


  


  


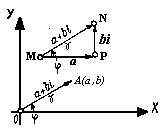
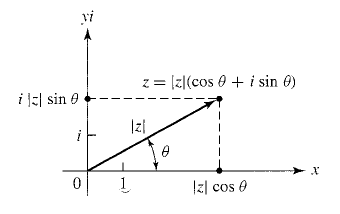
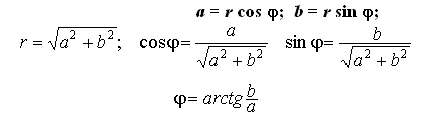
Число представляется в виде:
	a + bi

	r = sqrt(a^2 + b^2)
	a = r cos Ф
	b = r sin Ф
	



  
  Возведение в степень 
 


  


  


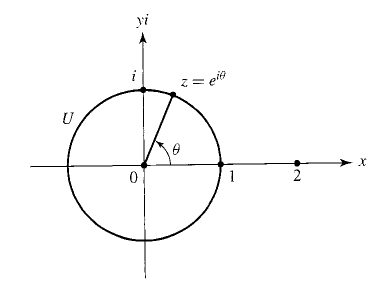
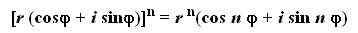
[ r (cos Ф + i*sin Ф) ]^n = r^n [cos(nФ) + i*sin(nФ) ]

e^(i*x) = cos(x) + i*sin(x)


Пример корней 4 степени из 1:
  



  


  


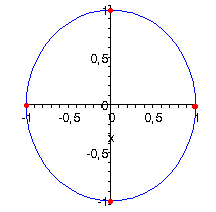
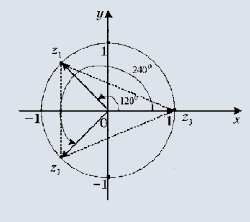
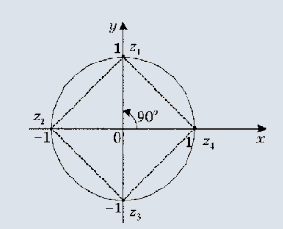
Комплексные числа широко используются в электроннике.


	ln(-1)   = i*PI
	ln(2)    = ln(2) + i*PI
	ln(-1/2) = -ln(2) + i*PI