3.3. СХЕМА ГОРНЕРА И ПРЕОБРАЗОВАНИЯ В ДРУГУЮ СИСТЕМУ СЧИСТЛЕНИЯ

	N = aK * p^K + ... + a2 * p^2 + a1 * p^1 + a0

можно представить в виде

	N = a0 + p * (a1 + p * (a2 + ... + p(a[K-1] + p*aK))..))




  


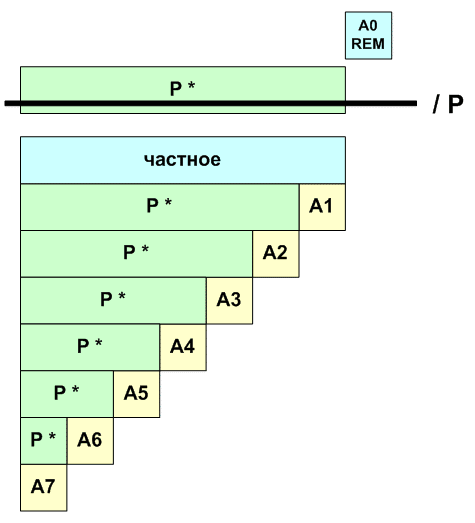
Схема Горнера - ключ к переводу чисел в другие системы счистления.

Пример:
	N = a0 + p * (a1 + p * (a2 + p * a3))
		
		делим N/p
		/     \
  ^	остаток       частное
  |	  a0	       a1 + p * (a2 + p * a3))   > p
  |		       делим на p
  |		      /       \
   \		   остаток    частное
     \		    a1         a2 + p * a3    > p
       \			делим на p
	 \			/      \
	   \		    остаток    частное
	     \		      a2         a3     < p
	       \
	          +----------------------------
			  берем остатки в этом направлении
			
	Число N = (a3a2a1a0) {p}



Пример:
	Переведем  3287 {10} в {7}
	Делим в столбик:

	3287|7
	----+---
    ^ 	   4|469|7
     \	     ---+--
       \       0|67|7
	 \	 --+-
	   \	  4|9|7
	     \	    -+- 	
               \    2|1
                 +-----

	3287 {10} =  12404 {7}



Другой пример:
	Перевод 100 {10} в {2}

	100| 2
^       ---+--
|	  0|50|2
|	    --+--
|	     0|25|2
|	       --+--
|		1|12|2
|		  --+-
|		   0|6|2
|		     -+-
|		     0|3|2
|		       -+-
|		       1|1
+---------------------------

	100 {10} = 1100100 {2}