3.3.1. ДРОБНЫЕ ЧИСЛА

Как получается дробная часть числа.
Все как обычно в позиционных сисиемах:

	(.a1!a2!a3!..)[n] = a1! * n^(-1) + a2! * n^(-2) .... итд


Для двоичной системы:
	-------------------
	.0	= 0
	.1	= 1/2

	.00	= 0
	.01	= 1/4
	.10	= 2/4 = 1/2
	.11	= 3/4


	.000	= 0
	.001	= 1/8
	.010	= 2/8 = 1/4
	.011	= 3/8
	.100	= 4/8 = 1/2
	.101	= 5/8
	.110	= 6/8 = 3/4
	.111	= 7/8
	-------------------

итд

  





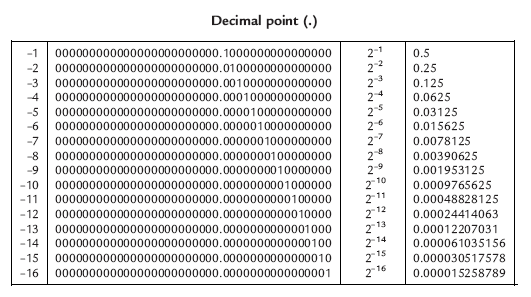
Для преобразования их в другую систему счисления:

Обоснование:
		A = c0 * b^-1 + c1 * b^-2 + ....
	      A*b = c0 (целое) + с1 * b^-1 + ...
         A*b - c0 = c1 * b^-1 + ...
   (A*b - c0) * b = c1 (целое) + ....


Пример 1:
	10.25 [10] = 10 1/4 [10] = 1010.01 [2]


Пример 2:
	3.75 десятичное в двоичную
	Целая часть	3 = 11
	Дробная
		0.75 * 2 = 1.50	 [1]	
		0.50 * 2 = 1.00  [1]
		0.00	   закончили

	Итак 3.75 = 11.11


Пример 3:
	57.45 дестичное в двоичную систему:

	Целое переводится как обычно  57 = 111001
	Переводим дробную часть.
	Только на этот раз не делим, а умножаем и берем целую часть.

		0.45  *  2  = 0.90	[0]	2^-1    MSB
		0.90  *  2  = 1.80	[1]	2^-2     ^
		0.80  *  2  = 1.60	[1]	2^-3     |
		0.60  *  2  = 1.20	[1]	2^-4     |
		0.20  *  2  = 0.40      [0]     итд      |
		0.40  *  2  = 0.80	[0]              V
		0.80  *  2  = 1.60	[1]             LSB
			и все повторяется т.е. переодическая дробь
	57.45 = 111001.01(1100)


Пример 4:
	10.23 десятичное в троичную систему

	целую часть:
		10 | 3
	3^0   -> 1 +---
		     3  | 3
	   3^1   ->  0  +---
	       3^2   -->  1

	целая часть = 101
	
	дробная часть.
		0.23 * 3  =  0.69	[0]	3^-1
		0.69 * 3  =  2.07	[2]	3^-2
		0.07 * 3  =  0.21	[0]	3^-3
		0.21 * 3  =  0.63	[0]	3^-4
		0.63 * 3  =  1.89	[1]	3^-5
		0.89 * 3  =  2.67	[2]	3^-6
		0.67 * 3  =  2.01	[2]	3^-7
		0.01 * 3  =  0.03	[0]	3^-8
		0.03 * 3  =  0.09	[0]	3^-9
		0.09 * 3  =  0.27	[0]	3^-10
		0.27 * 3  =  0.81	[0]	3^-11
		0.81 * 3  =  2.43	[2]	3^-12
		0.43 * 3  =  1.29	[1]	3^-13
		0.29 * 3  =  0.87	[0]	3^-14
		0.87 * 3  =  2.61	[2]	3^-15
		0.61 * 3  =  1.83	[1]	3^-16
		0.83 * 3  =  2.49	[2]	3^-17
		0.49 * 3  =  1.47	[1]	3^-18
		0.47 * 3  =  1.41	[1]	3^-19
		0.41 * 3  =  1.23	[1]	3^-20
		0.23 * 3  =  0.69	[0]	3^-21  повторение - дробь циклическая

	таким образом
		10.23 {10} = 101.(02001220000210212111) {3}