3.16. НЕМНОГО ОБЩЕЙ АЛГЕБРЫ

  



  
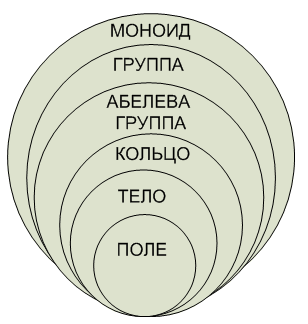
  Группа 
 


Def
===
	Множество G с заданной на нем бинарной операцией @ назовем ГРУППОЙ
	если выполняются следующие аксиомы:

	1) Ассоциативность
	   Для любых a,b,c из G:
		(a @ b) @ c = a @ (b @ c)
	2) Наличие нейтрального элемента
	   В G существует элемент е такой, что для всех a в G
		e @ a = a @ e = a
	3) Наличие обратного элемента
	   для любого a из G есть обратный элемент b такой, чтo
		a @ b = b @ a = e

	(Если выполняются только первые 2 аксиомы то такое множество 
	 называется МОНОИДОМ)



Def
===
	Если группа еще и коммутативна
	т.е. для всех a,b из G
		a @ b = b @ a
	то такая группа называется АБЕЛЕВА ГРУППА



  
  Кольцо 
 
Def
===
	Множество G c заданными на нем бинарными операциями '+' и '*'
	называется КОЛЬЦО если выполняются следующие аксиомы:

	1) Коммутативность по сложению
	   для любого a,b в G
		a + b = b + a
	2) Ассоциативность по сложению
	   для любого a,b,c в G
		a + (b + c) = (a + b) + c
	3) Наличие нейтрального элемента по сложению (нуля)
	   В G существует элемент 0 такой, что для всех a в G
		a + 0 = 0 + a = a
	4) Дистрибутивность
	   для любых a,b,c в G
		a * (b + c) = b * a + c * a


	Дополнительные свойства возможные у колец:
	5) Коммутативность по умножению
	   для любого a,b в G
		a * b = b * a
	6) Ассоциативность по умножению
	   для любого a,b,c в G
		a * (b * c) = (a * b) * c
	7) Наличие нейтрального элемента по умножению (единицы)
	   В G существует элемент 0 такой, что для всех a в G
		a * 1 = 1 * a = a
	8) Отсутствие делителей нуля
	   для любого a,b в G
	   если  a * b = 0
	   то как минимум либо a = 0, либо b (либо оба)

Примеры колец:
	Z  - целые числа
	Zn - кольцо вычетов по модулю натурального числа n
	R[x1,...,xn] - кольцо многочленов от n переменных над полем R



  
  Тело 
 
Def
===
	Ассоциативное по умножению кольцо с 1 (т.е (6)+(7)) в котором каждый
	ненулевой элемент обратим
	т.е для любого ненулевого a из G - существует ненулевой b из G
	такой что
		a * b = b * a = 1
	называется ТЕЛОМ


Пример тел:
	Квадратные матрицы
	Кватернионы




  
  Поле 
 
Def
===
	Коммутативное (5) тело называется ПОЛЕМ

Примеры полей
	Q - рациональные числа
	R - вещественные числа
	С - комплексные числа
	Zp - поле вычетов по модулю p, где p - простое число
	Fq - конечное поле из q = p^k элементов где p - простое число,
	     a k - натуральное