3.16.2. ВЕКТОРНАЯ АЛГЕБРА

Def
===
	ВЕКТОР - это направленный отрезок

	Два вектора равны если их отрезки паралельны, имеют одинаковую длинну
	и направление.

	Длинна вектора - это длинна соответствующего отрезка.



  
  Сложение 
 
  

		->                      ->
		a  = { x1, y1, z1 }	b  = { x2, y2, z2 }

		->  -> 
		a + b  = { x1+x2, y1+y2, z1+z2 }

		->  ->
		a - b  = { x1-x2, y1-y2, z1-z2 }



  
  Скалярное произведение 
 

	        -> ->    -> ->
		a  b  = |a| |b| cos Ф

	для декартовых координат
		->                      ->
		a  = { x1, y1, z1 }	b  = { x2, y2, z2 }

		->  ->
		a * b  = x1*x2 + y1*y2 + z1*z2




  
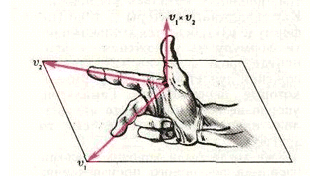
  Векторное произведение 
 

	Результат векторного произведение векторов  -  вектор который имеет длинну
	              -> ->
		R  = |a| |b| sin Ф

        ортогонален векторам a и b
        и тройка abc является правой.
  


	для декартовых координат
		->                      ->
		a  = { x1, y1, z1 }	b  = { x2, y2, z2 }

		->  ->
		a X b  = { y1*z2 - y2*z1, z1*x2 - z2*x1, x1*y2 - x2*y1 }


		->  ->       |  i   j  k  |
		a X b  = det | x1  y1 z1  |
			     | x2  y2 z2  |



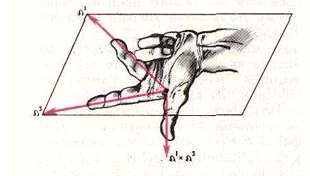
Операция верторного умножения не является коммутативной:
	т.е.
	        ->  ->       ->   ->
		a x b   !=   b  x a    (в общем случае)